College Mathematics Journal, 27 (1996) no. 3, 186-192.
| Copyright The Mathematical Association of America |
Problem A-6 of the 53rd Putnam Competition read as follows:
Four points are chosen at random on the surface of a sphere. What is the probability that the center of the sphere lies inside the tetrahedron whose vertices are at the four points? (It is understood that each point is independently chosen relative to a uniform distribution on the sphere.)
The problem has a geometric immediacy that makes it tantalizing: the tetrahedron so formed is readily visualized and no great mathematical background is necessary to understand the question being asked. Further, it is almost impossible to resist the urge to generalize the problem. Some of the variants that spring to mind quickly are:
Despite the fact that the original Putnam question is so easily understood, the solution is (not surprisingly) not arrived at with equal ease. This sentiment is supported by the fact that 123 of the top 203 scorers on the Putnam exam submitted no solution at all to problem A-6, and a relatively low number of 9 of the top scorers received a full 10 points for the problem. This difficulty in answering such an easily grasped problem just makes it more intriguing, of course, and suggests that the problem and its generalizations are worth investigating. In this paper we will develop a surprisingly simple answer to questions (1) and (2). In addition, our result answers rather general forms of questions (3) and (4).
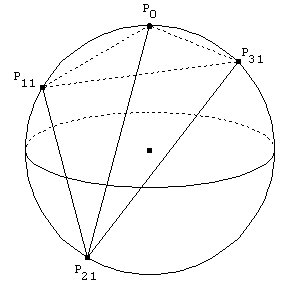
In [3], Klosinski, Alexanderson and Larson offer the following solution to A-6. Assume the sphere is centered at the origin, and that the first point P0 is located at the north pole of the sphere, with the three remaining points then located at random locations on the sphere. We can assume that these remaining points are chosen in a two-step process: first a diameter Pi1Pi2 (i Î {1,2,3}) is fixed and then one of the two end-points {Pi1,Pi2} is selected as a vertex of the tetrahedron. Figure 1 below illustrates a typical orientation of the choices. The eight possible tetrahedra P0P1j1P2j2P3j3 (with each ji being 1 or 2) are equally likely. Further, we can assume that the result is an honest tetrahedron and that the origin does not lie on any face. (Recall that the plane through three noncollinear points P1, P2 and P3 consists of all affine combinations
|

In particular, the four vertex vectors
|
|
|
|
|
Each point in the tetrahedron with vertices P0, P1j1, P2j2,P3j3 can be uniquely represented as a convex combination
|
|
So far, so good. This solution generalizes in the obvious way and gives us the answer of 1/2n to question (1) in the above list. But what of question (2)? The above approach seems inadequate in this case, since points can now be chosen anywhere along the randomly chosen diameters.
Let us employ one of the standard procedures when faced with a difficult problem: that of changing the problem to something easier. We will attempt first to answer question (2) in R2. Specifically, if three points are chosen at random from the unit disk B2, what is the probability that the triangle thus formed contains the origin? Let us further simplify the problem by assuming that we are choosing three points at random with respect to a probability measure P on B2 which is rotationally invariant ; that is, measures of subsets of B2 are unchanged under rotational translations. We will also continue to assume the appropriate degree of non-degeneracy of the measure (more on this in the next section).
Since we are assuming rotational invariance, we can assume that the first point P1 is fixed between 0 and 1 on the positive x-axis. With probability one, the second point P2 of the triangle is not located at the origin, and we can form the ray starting at the origin and passing through P2. Let q be the angle between the positive x-axis and this ray. The question can now be posed as a conditional probability problem: given q, what is the probability that the third point P3 defines a triangle which contains the origin? Integrating this probability over all possible q's will then give us the answer we seek.
In order to simplify our work, let us agree upon some notation. Given a point P in B2 -{(0,0)}, let Q(P) denote the angle from the positive x-axis to the ray beginning at the origin and passing through P (see Figure 2). Thus, q1 £ Q(P) £ q2 will indicate that P lies in the sector of B2 defined by the angles q1 and q2. Let P(capture) denote the probability that the origin is captured within the triangle formed by the three points P1, P2 and P3. Thus, the first task is to calculate P(capture | Q(P2) = q), for each q Î [0,2p].
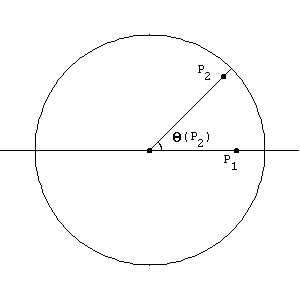
Suppose first that 0 £ q £ p. It is not difficult to see that a necessary and sufficient condition for capture is that p £ Q(P3) £ p+ q. That is, the ray from the origin to P3 must pass through S1 (the boundary of B2) at a point between p units and p+ q units, as measured from the positive x-axis. Since the length of this arc is q, this conditional probability is q/2p, i.e. P(capture | Q(P2) = q) = q/2p. Similarly, if p £ q £ 2p, P(capture | Q(P2) = q) = 1 - q/2p.
We can now approximate our solution with an appropriate Riemann sum. Let { q0, ¼, qn } be a partition of [0,2p]. Then
|
In the limit of finer and finer partitions, we obtain
|
Examination of this argument shows that we have answered more than we set out to, since the fact that P is a probability measure on B2 is really irrelevant. As long as P is a probability measure on R2 which is rotationally invariant and suitably non-degenerate, the result is the same. We are already aware of one consequence of this: if P is a uniformly distributed probability measure on S1, the method of Klosinski, Alexanderson and Larson tells us that with probability 1/4 the origin will be contained in a randomly chosen triangle. We can also begin to make sense of question (4) by noting that if P is the usual Gaussian probability measure on all of R2, the probability that three randomly chosen points captures the origin is again 1/4.
A related problem in geometric probability, whose many variants are dealt with in [1], [2], [4], [5] and [6], is to find the probability that three points chosen at random from a region in the plane will form an acute triangle. One version can be easily answered here. Since the origin is captured by three points chosen at random from the unit circle if and only if the three points form an acute triangle, the probability that an acute triangle is formed by three points chosen at random from S1 is also 1/4.
The results above suggest that under rather general circumstances n+1 points chosen randomly from a region in Rn which is symmetric with respect to the origin will capture the origin with probability 1/2n. Our main result gives conditions which guarantee the validity of this conclusion, and thus provides answers to questions (2), (3) and (4).
We begin with a theorem, in which we finally describe the amount of non-degeneracy of the measures that we require. We also discard rotational-invariance for a weaker condition.
Theorem 1 Let Rn be endowed with a probability measure m which is symmetric with respect to the origin and such that when n+1 points are chosen independently with respect to m, with probability one their convex hull is a simplex. Then the probability that the origin is contained in the simplex generated by n+1 such random points is 1/2n.
Recall that a measure m is symmetric if m(-S) = m(S) for any measurable set S. Also, n+1 points x1,x2,¼,xn+1 from Rn are vertices of a simplex if and only if none of these points lies on a hyperplane containing the other n points. Thus simplexes in R2 are triangles and simplexes in R3 are tetrahedra.
As examples of how the theorem can be applied, we could let m be a uniformly distributed probability measure on a rectangle centered at the origin in R2, or on the boundary of such a rectangle. In either case, if three points are chosen at random with respect to the measure, the probability that the origin is contained in the triangle thus formed is 1/4. In R3, the original Putnam answer of 1/8 applies to four points chosen at random from a cube, or from the surface of a cube, as well as from the sphere. More generally, let D be any domain in Rn with finite volume and which is symmetric with respect to the origin. Then the probability that the origin is in the convex hull of n+1 points chosen uniformly and independently from D is 1/2n. Note that, as in Figure 3, it is not necessary for D to contain the origin, or even for D to be connected.
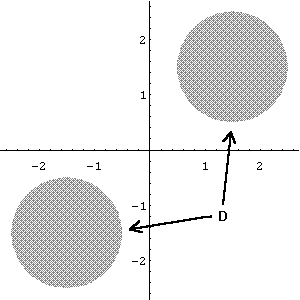
We will now proceed with the proof of the theorem.
Proof: Begin by defining a new probability space W = Rn ×¼×Rn (n+1 factors) with the product measure m×¼×m. Let
|
For each set of indices I Ì {1, ¼, n+1} let
|
|
Our proof now rests on four observations.
To prove (i), suppose w Î AI, with w = (x1, x2, ¼, xn+1). Then wI Î A, i.e.
|
|
|
Next, let x1, ¼, xn+1 be chosen independently with respect to m from Rn, and let w = (x1, ¼, xn+1). Because of the hypothesis that with probability one none of the random points xi is in the hyperplane spanned by the other n points, the origin has a representation as an affine combination of x1,x2,¼,xn+1 that is almost surely unique, say
|
Observation (iii) follows from noting that for any n+1 randomly chosen points x1,x2,¼,xn+1 from Rn, the zero vector can be expressed as an affine combination of these points, and the set AI = AIc which contains w = (x1,x2,¼,xn+1) is essentially uniquely determined by this expression. Finally, (iv) follows from the hypothesis that m is invariant under reflection through the origin, so that for any index set I the mapping w® wI on W that changes the signs of the coordinates in I preserves the product measure. This mapping sends AI onto A, so m(AI) = m(A) for all I.
The index set Á = {I | I Ì {1,¼,n+1}} has 2n+1 elements, but AI = AIc so our claims show that W can be written as an essentially disjoint union of 2n subsets each with the same measure. Thus each of these subsets has measure 1/2n. In particular A has measure 1/2n, completing the proof of the theorem. ¨
After discovering the above proof, we learned that our result for points chosen from the surface of the unit sphere in Rn could be deduced from a result due to J. G. Wendel and found in [8]. Wendel showed that if N points are chosen at random from the surface of the unit sphere in Rn, the probability that all N points lie in the same hemisphere is given by
|
If we let N = n+1, then the probability that the origin is contained in the convex hull of n+1 points chosen at random from the unit sphere in Rn is 1 - pn,n+1, which as the reader can verify is 1/2n. A referee pointed out another interestingly odd result related to our investigation that can be found on page 124 in [7]: If five points are chosen at random from a ball in R3, the probability that one of them is contained in the tetrahedron generated by the other four is 9/143.