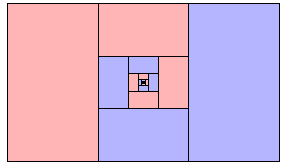
Several years ago, when my daughter was in the third grade, I decided it was time she learned about geometric series. After all, she had just been introduced to fractions in school, so she was obviously ready. The two of us were just finishing a meal at a restaurant and were about to have some chocolate cake for dessert when what follows took place. (Now please realize that I was rather full of dinner, and this was a few years ago, so some of the details might not be 100% historically accurate. But that just makes the story better.)

"Samantha," I began, "Have you learned how to add fractions yet?"

"No, Dad. Are we going to have the cake now?"

"Well no matter, I'm going to show you how to add lots of fractions. It's very easy. If you will listen to me carefully while we talk about infinite sums, then we'll have our cake."

"Okay, sure!" she readily agreed. She obviously shares her father's love of math.

I had selected a very large, rectangular slice of chocolate cake for us to share, and it sat on a plate in the center of the table. I asked the waitress for two more plates. When they arrived I began my presentation.

"Now Samantha, you are just a little girl and I really don't think you can eat as much cake as me, so first I will cut the cake into thirds," which I proceeded to do. "If you can finish your third, then you can have some more. You understand thirds, right?" She nodded, and I could tell by her expression that she understood thirds. I placed one piece on my plate, one on my daughter's and left the third between us on the third plate.

"Now I'll cut the remaining third into thirds. That makes each piece one-ninth of the original, doesn't it?"

"Mmmmm!" she agreed, her mouth already full. I could see they had taught her well in school and I was very proud. I continued with a brief review of the algebra of fractions as Samantha polished off her first portion. Everything was going according to plan.

"Okay, Sam, now you can have one third of a third, and I'll take one. And I'll cut the remaining third of a third into thirds again. The pieces are getting pretty small now, aren't they? These pieces are thirds of ninths, so that makes...?" I waited. Samantha looked up from her cake. Her mouth was full again, so I helped, "... twenty-sevenths." Sam nodded in full agreement.

"Now Sam," I continued, "every time we divide the pieces and take our share, who gets more cake, me or you?"

When it comes to the fair division of cake, kids are very sharp. "We both get the same amount every time," she said.

"Right! And now imagine that we keep doing this forever, always taking thirds of what is left. How much cake will be left?"

"Not much after a while. Just crumbs."

"Well, not even crumbs after a while. We just keep cutting and cutting..." I sensed I had better postpone discussing the notions of convergence or the possible magnitude of an arbitrarily small nonnegative quantity.

"So look, Sam. We each got the same amount of cake, right? And there is nothing left after awhile."

"Almost nothing," she corrected.

"Okay, but we keep cutting forever, so there's really nothing left..." I didn't want to get into technicalities with a child. Trying not to lose my patience, I offered a practical analogy. "Now look Sam, if I took the whole piece of cake at the beginning and cut it in half, there would be crumbs. But you'd still agree that each piece was half the cake right?"

"Yeah, I guess so. Almost a half, except for the crumbs."

"Yes, yes, very well, but you're missing the point. Let's return to our cake. We each got one third and then a third of a third and then a third of a third of a third and so on. Each of us gets the same amount and eventually the cake is gone. So each of us gets half the cake. You see, Sam? It means that one third plus one ninth plus one twenty-seventh, etc., adds up to one half! Don't you see it?" She nodded politely but had a rather sad look. It dawned on me then that I had overdone it, expecting a little kid to understand such subtle things. She obviously felt she had disappointed me. What had I done? She would probably start hating fractions and math now. (Being a college math professor, I had a sense of déjà vu.) I admit I was a bit disappointed. I thought the whole idea was so simple that even a third-grader could get it.

"Dad?"

"Yes, Samantha?"

"Aren't you going to eat your half?"

(The above picture is printed as ``Mathematics Without Words," in the College Journal of Mathematics, 32, no. 1 (2001), p.19.)