1 3 + 1 9 + 1 27 + ⋅⋅⋅ = 1 2

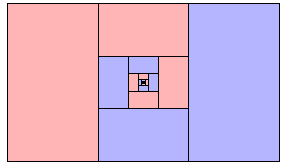
one could get carried away. Here is one I like okay:

1 4 + 1 42 + 1 43 + ⋅⋅⋅ = 1 3

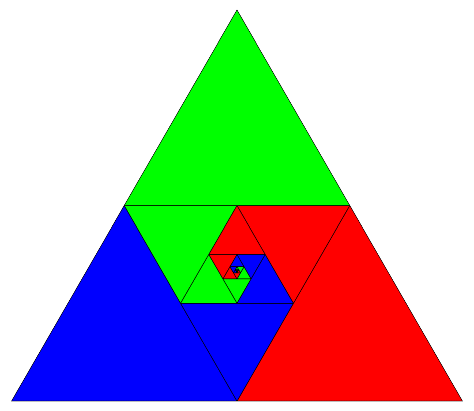
And now I realize I have actually seen the following in the calculus text we use:

1 8 + 1 16 + 1 32 + ⋅⋅⋅ = 1 4

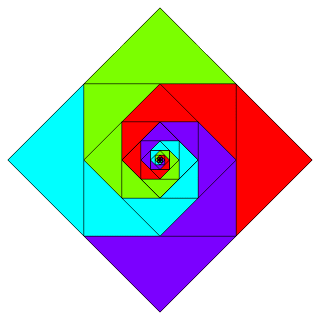
(Of course, nobody needs much of a picture to understand the above equality.) How far can you go with this? I hoped to find something interesting by exploiting these analogs...

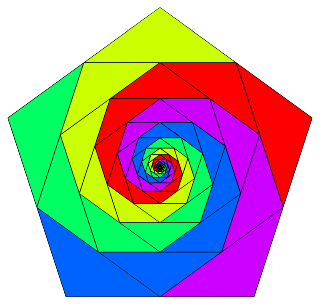
but all I obtain from considering general N-gons is the rather lame identity that follows. (And it's derivation from the picture is hardly without need of explanation.)

&infin ∑ k = 0  (cos2 π/N)k = csc2 π/N

I suppose it is a decent exercise for a student to find the common ratio of triangle areas...

Rick