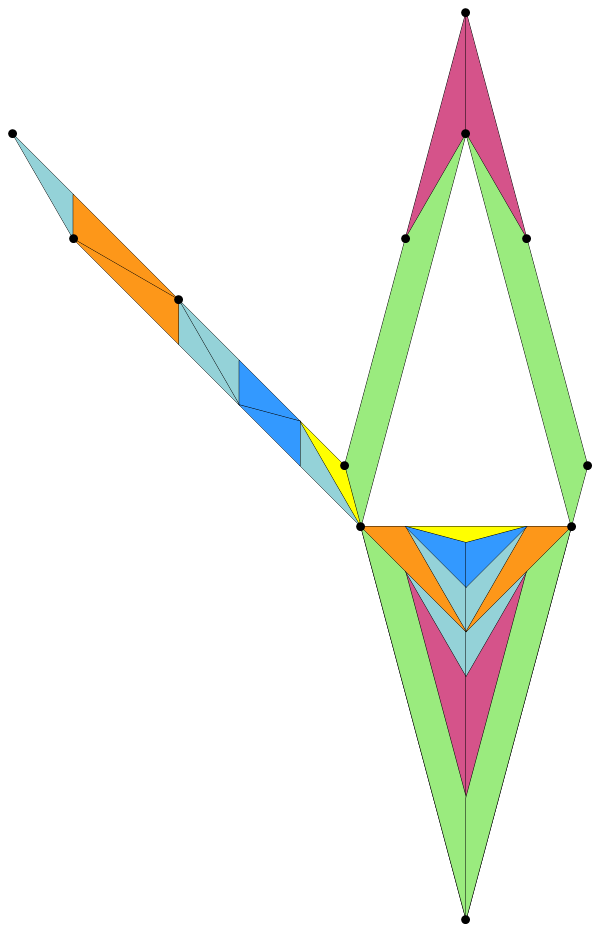
What the heck is this thing? A crossing guard?

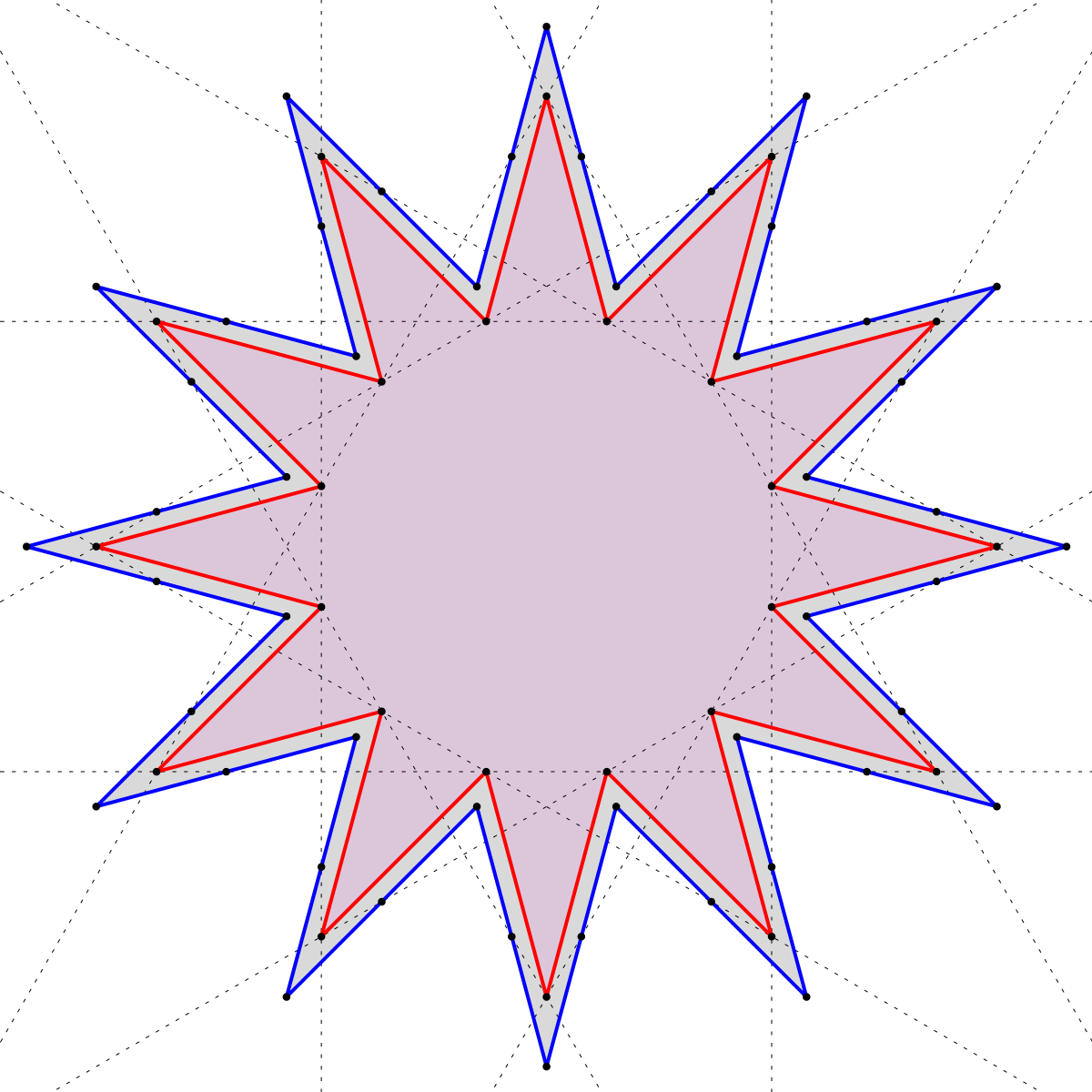
Assume below that what look like midpoints of the segments of the outer {12/5} dodecagram (blue outline) are indeed midpoints. Connecting them (every seventh segment; see the uppermost horizontal cross-cut) creates an inner {12/5} (red outline) that has three-fourths the area of the outer one. That is,

3×outer=4×inner.

An analytic proof of that is easy. But for OCD reasons we would like a dissection that is somehow generated or related, especially one that does not move the inner {12/5}.

Here is how:

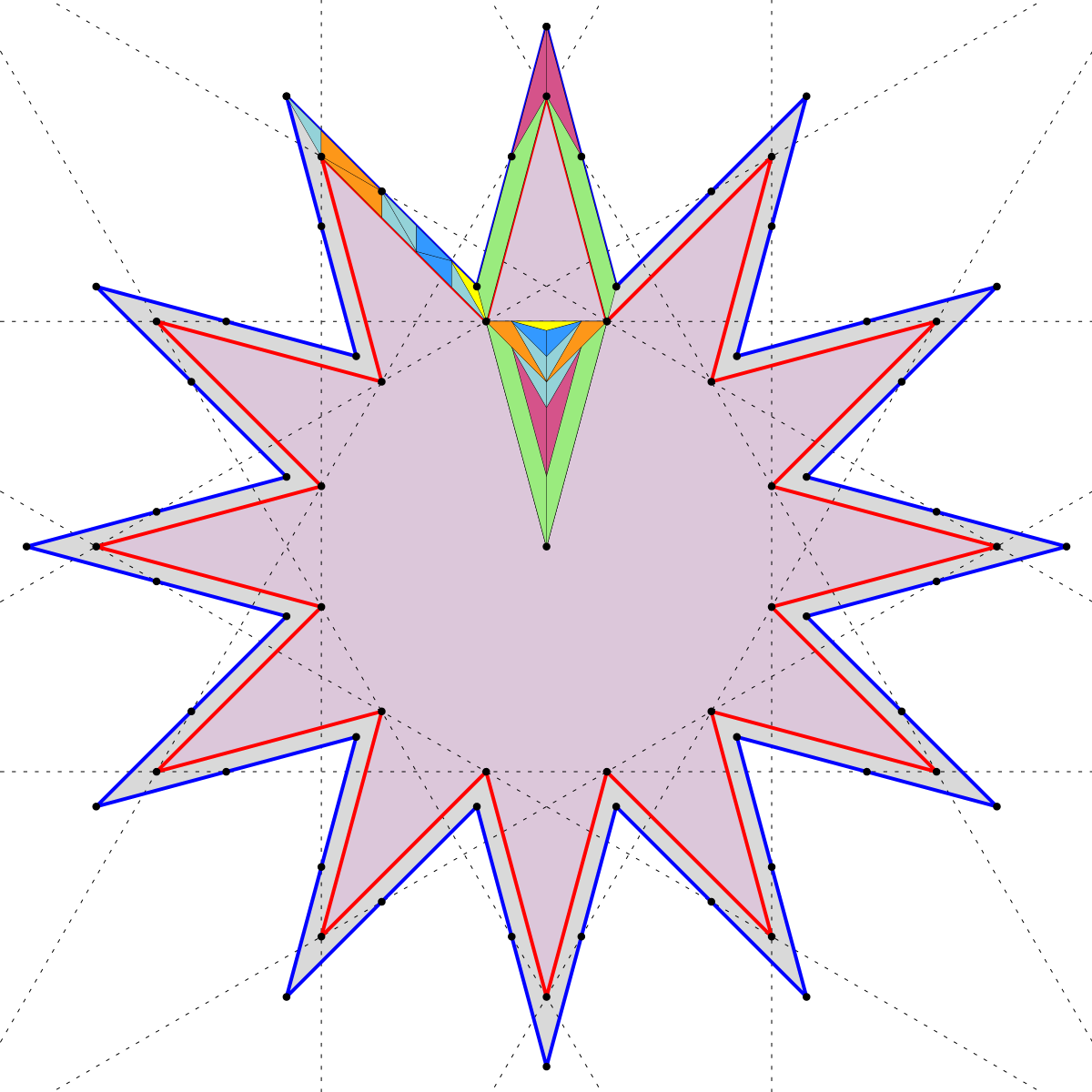
That's a visual demo, but maybe too subtle to be enjoyable. An explicit version is below, but to get it to fit nicely on the screen causes the details to be lost. The effect is still clear, one hopes.

3 = +3