Below are a few graphic examples of certain "ambiguous" unfoldings of polycubes "1x1x3" and "L1" along with a bit of data. Some terminology is explained further ahead.
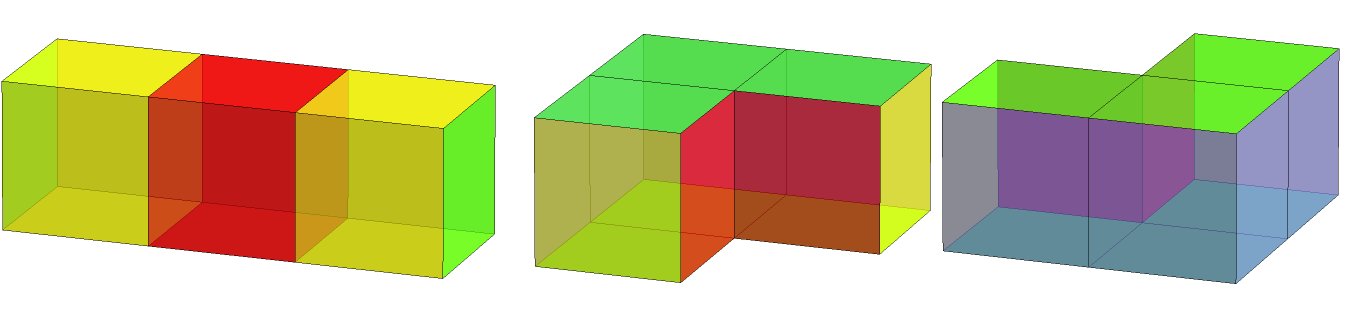
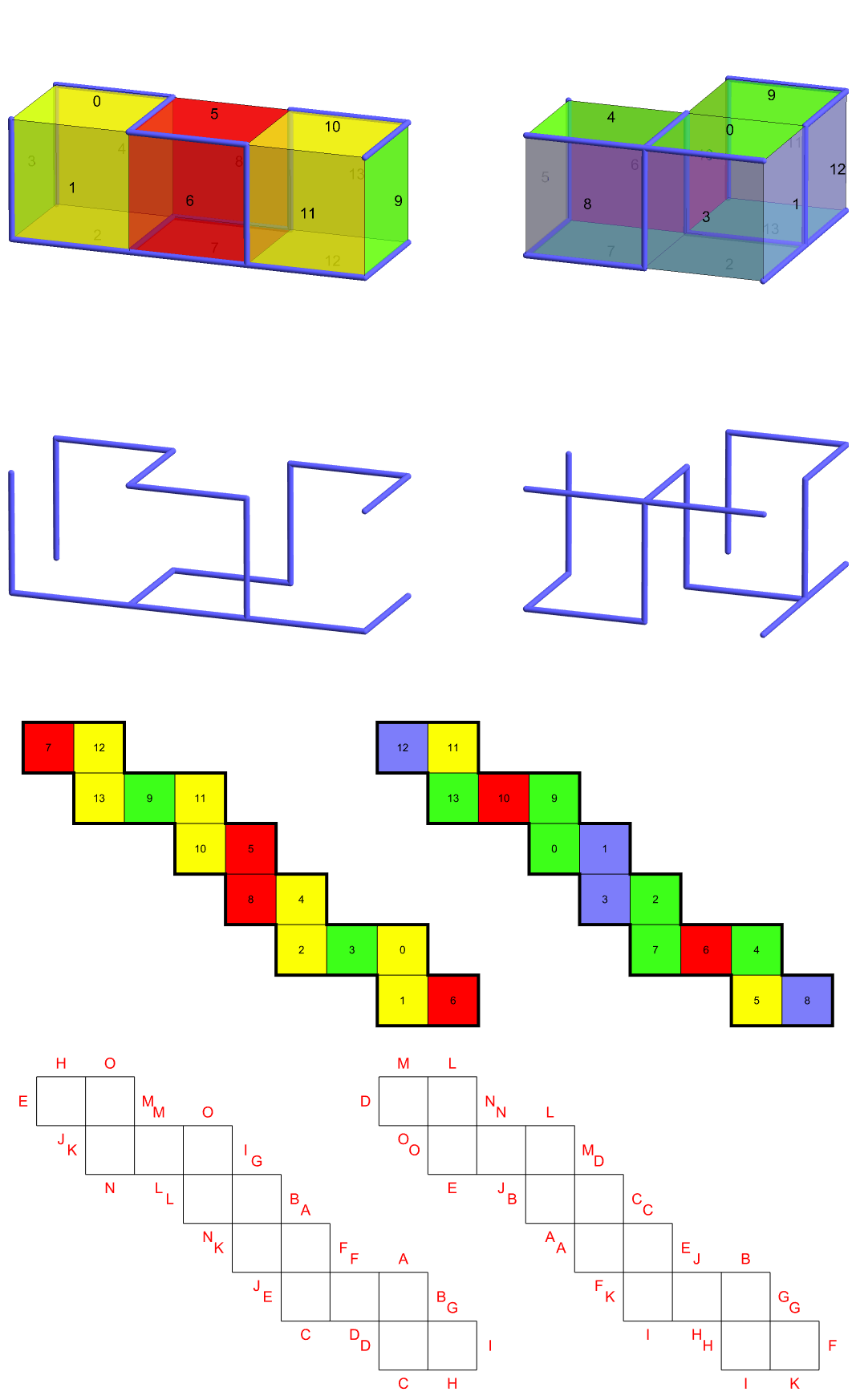
First are simple depictions of the two "3-cubes" or tricubes — the only polycubes Wikipedia with 3 cubes. The first image is what we'll call "1x1x3"; the other two are front and back views of "L1", the smallest L-shaped polycube. The colors are used to mark different portions of the two polycubes.

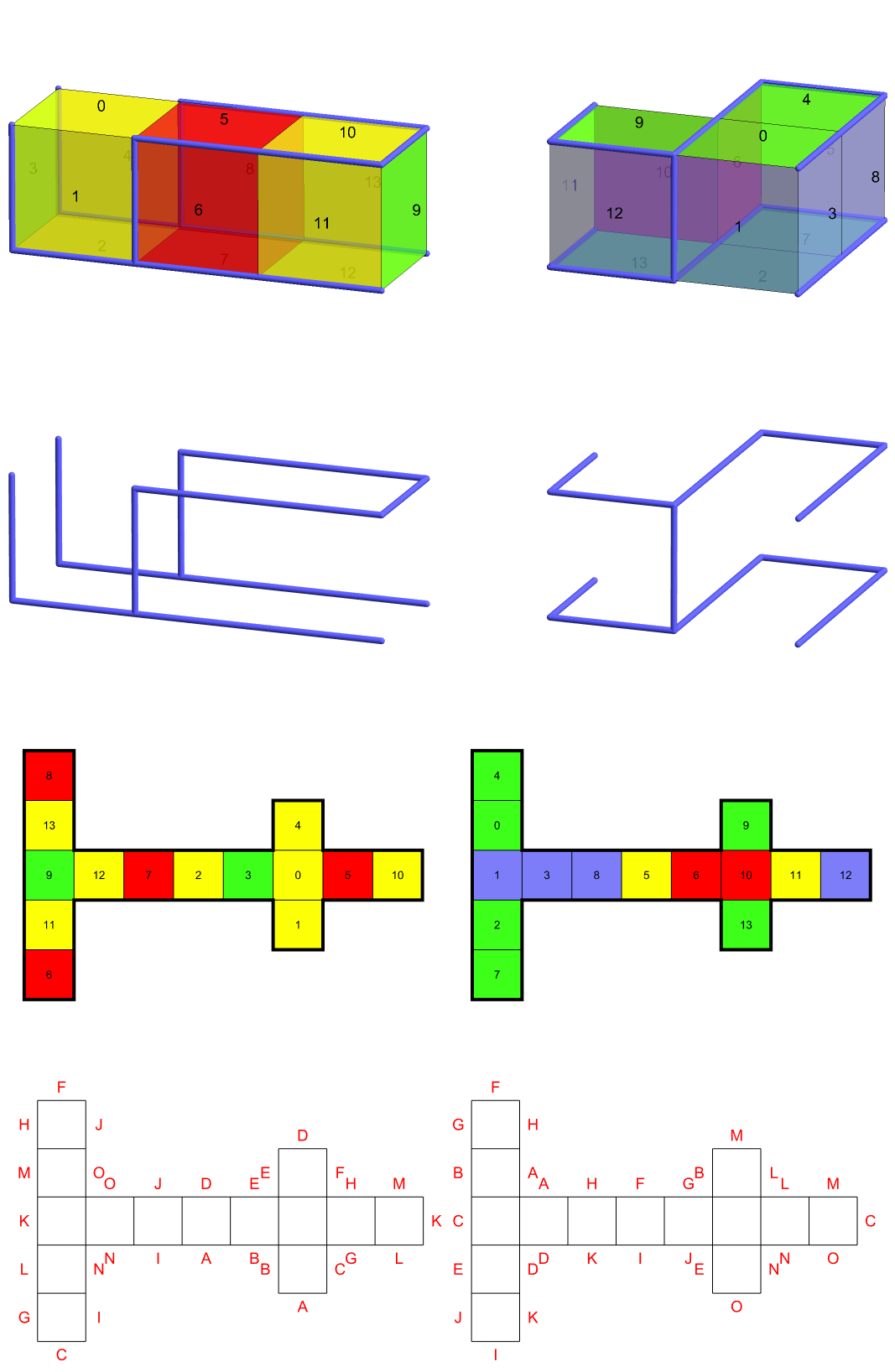
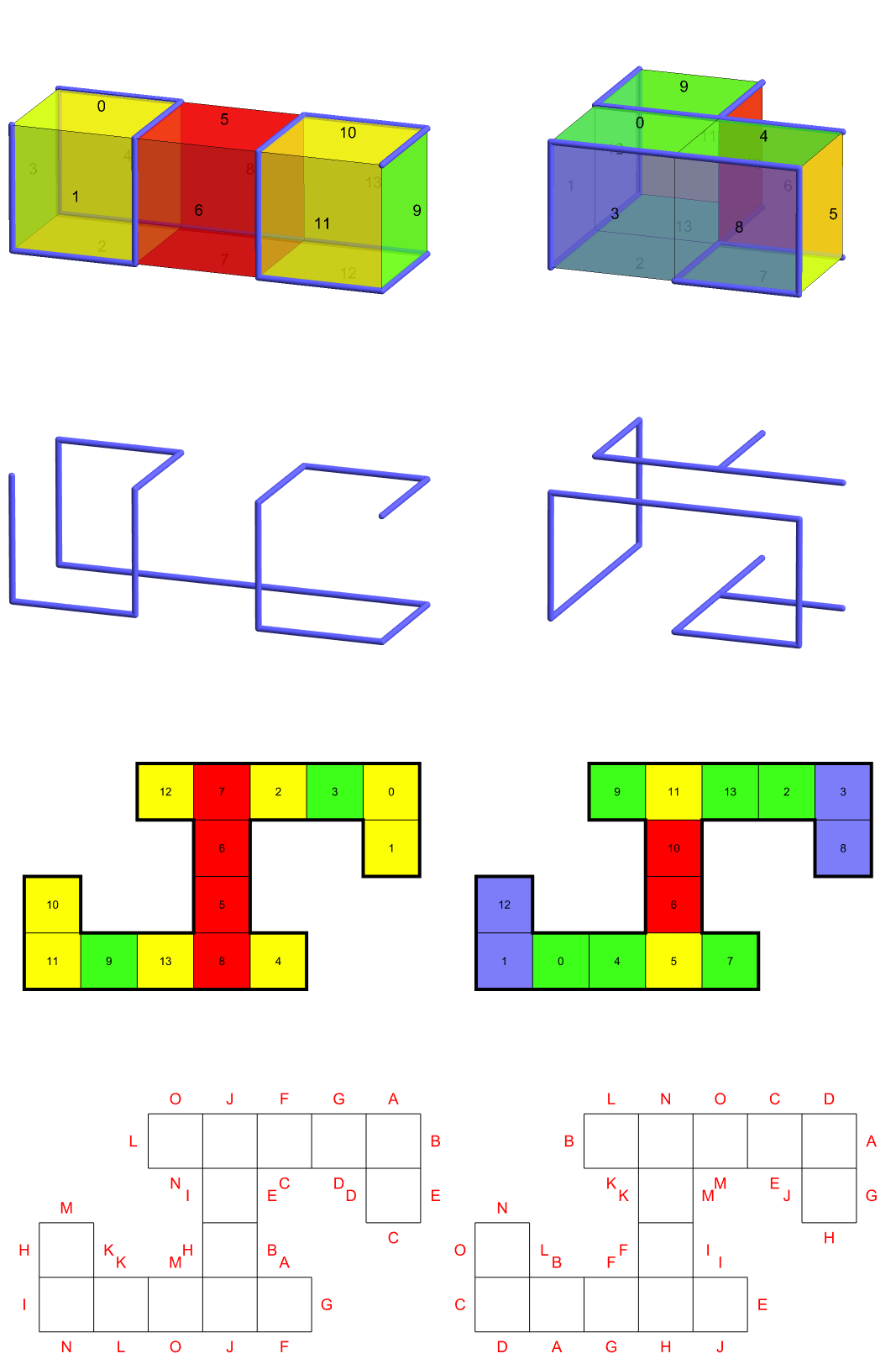
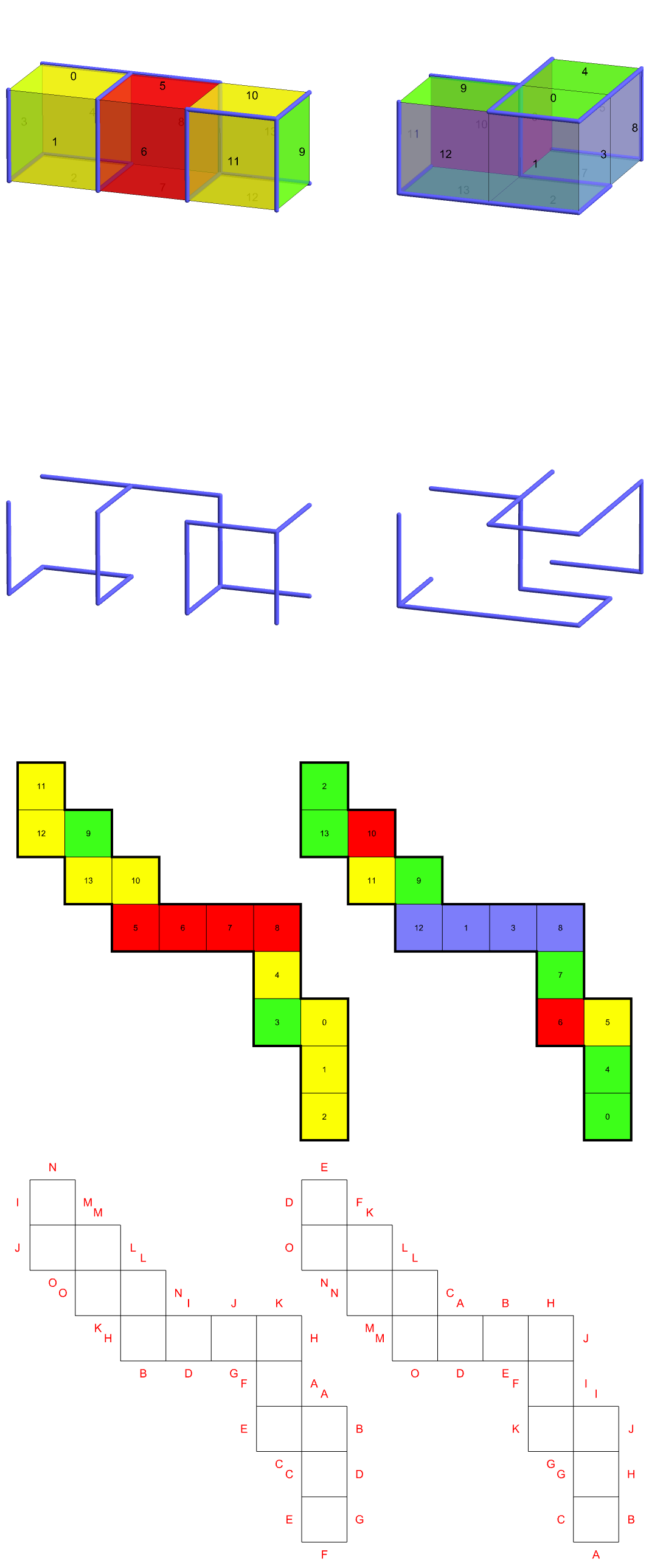
A variety of ambiguous examples follow, with four pics and a video each. The first net has bilateral symmetry, the second has point symmetry, the third is serpentine, the fourth is serpentine with point symmetry. The 1x1x3 version of the second has a cut tree that is a Hamiltonian path, resulting in a zipper unfolding.
| 1x1x3 | L1 | |
|---|---|---|
| labeled spanning trees | 2387552 | 2382359 |
| distinct cut trees | 160256 | 622640 |
| distinct unfoldings | 160114 | 567030 |
| distinct simple nets | 6173 | 36368 |
| distinct serpentine nets | 567 | 2103 |
| distinct simple serp. nets | 75 | 479 |
| distinct zipper unfoldings | 265 | 824 |
| distinct simple zipper nets | 65 | 103 |
There are 28833 distinct (*) ambiguous unfoldings in the plane for this pair. Among those are 2160 ambiguous simple nets. Among those, 7 are serpentine. None are zippers.
(*) To say "distinct" means geometrically distinct, so the number of distinct cases is the number of congruence classes among the labeled spanning trees, congruence being in three dimensions for the corresponding cut trees, two dimensions for unfoldings into the plane.
The spanning trees are those of the face graph of the polyhedron.
By calling an unfolding "ambiguous" we mean that the unfolding can be re-folded into different polyhedra (here those polyhedra are the two 3-cubes in question). We should perhaps call this inter-ambiguity, as opposed to intra-ambiguity. (Elsewhere, I have often referred to the "intra" versions as freaks.
Calling an unfolding a net means the interiors of the faces of the unfolding do not overlap in the plane. A simple net is simple in the sense of a polygon: no edges or vertices of the net overlap (except, of course, on the edges that join the faces). A serpentine unfolding is one for which the spanning tree is a Hamiltonian path.
Regarding "inter-ambiguity" versus "intra-ambiguity", what we have, in the former (as shown above) is a net (or more generally, an unfolding) that can be folded up into different polyhedra. By "intra-ambiguity" we mean that the folding up results in the the same polyhedron, but in different ways. One way to put it is that the "gluing labels" can be geometrically distinct (in the two dimensions of the plane of the unfolding) but result folds up into the same polyhedron. Another view, for either type of ambiguity, is that the cut-trees are geometrically distinct (in three dimensions) but that the development folds out into the same plane polygon.
In the "intra" type, the squares from different parts of the polyhedron land in geometrically distinct places in the unfolding. To the extent that this can happen with our two polycubes, have a look at the following example, which involves only one net that folds up (to either L1 or 1x1x3) in nine different ways. (The colors should help with the intra-ambiguous cases.)