That's called "Living on the edge."

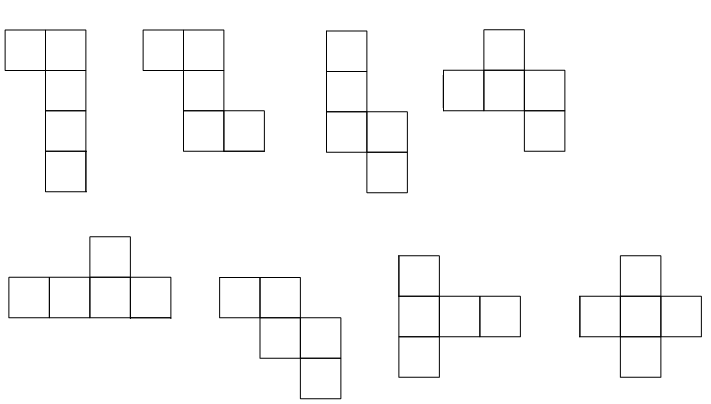
The figure above is built to suggest a three-dimensional tiling using nets of the cube. In this case, the nets are all congruent (#8 in my numbering of the 11 such nets).

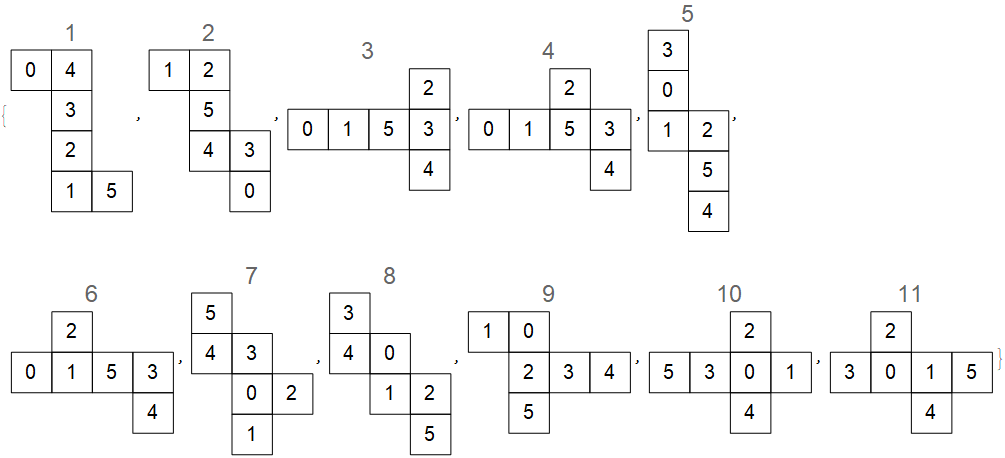
But as a plane figure (which of course it is!), it is a tiling using certain corresponding 12-iamonds. Let's call the top one below (as in the tiling above) a type-1 perspective of the net, the lower one type-2.

What I like about the three-dimensional version above is that the walls meet to produce a "step". Here is a more boring version, with no step, of those same nets, but from a type-2 perspective.

Puzzle 1. Is there a type-2 version with a step? But here is the catch: One can take the type-1 figure above and simply view it from a type-2 perspective, but then many of the faces are obscured, and of course we consider that a no-no!

Puzzle 2. What other type-1 stepped versions can be made with that net? In particular, can more exotic steps be made?

Puzzle 3. What sorts of stepped versions can be made with each of the individual remaining nets of the cube?

Puzzle 4. What sorts of stepped versions can be made that simultaneously use as many of the 11 nets of the cube as possible?

In the plane, all 11 nets can form a supertile, so wouldn't it be cool if there were such a thing that could make a 3D version like the one above?

Each of the puzzles above extend to polyominoes of any order. The cube nets are simply my favorites for such things, for reasons seen in the animation below.

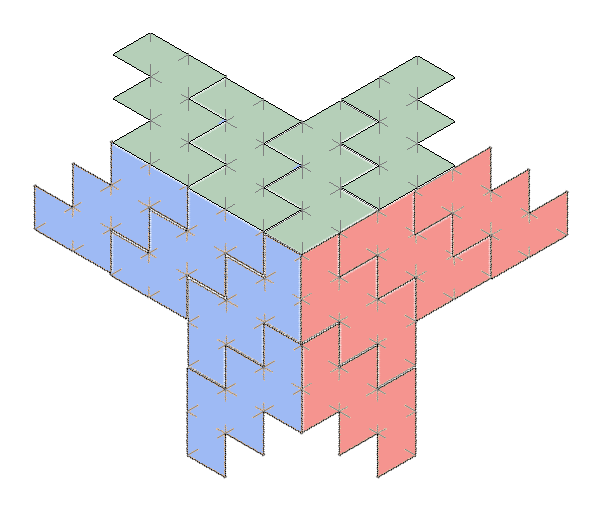
For a big old mix of polyominoes in perspective, one has to admire the creation of Ghee Beom Kim on the Mathematical Tiling and Tessellation Facebook group.

You can see in that dazzling image the nets that appear in my simple creation above. I merely took that same triple as a starting point.

This animation below is based on the tiling shown at the outset and presents a different sort of puzzle... The pauses at the beginning, end, and middle are 5 seconds each (the other stops are 2 seconds) and you can stop the video to check things out. The middle stop is the first image on this page. As the video cycles from the last image to the first, it abruptly goes from cubes "closed forward" to "closed backward". You'll see. A transition would help, but this is interesting in its own way. If you are looking at a particular cube when this happens and you note its base, you can see that the base does not change.

Puzzle 5. Given a cube-net tiling of a perspective type, choose the bases of the folding cubes so that the result is a stepped figure without obscured faces. The animation above achieves this and does so when the cubes are opened forward or backward! This took a lot of labor and was not very scientific. But it actually works for the infinitely tiled version, a larger portion of which is shown below in those two states. This is, of course, just a matter of taste, an extra challenge. Some cool versions with staircases running in other crazy directions can be made. Choosing the bases at random is still amusing enough.

Closed to the front:

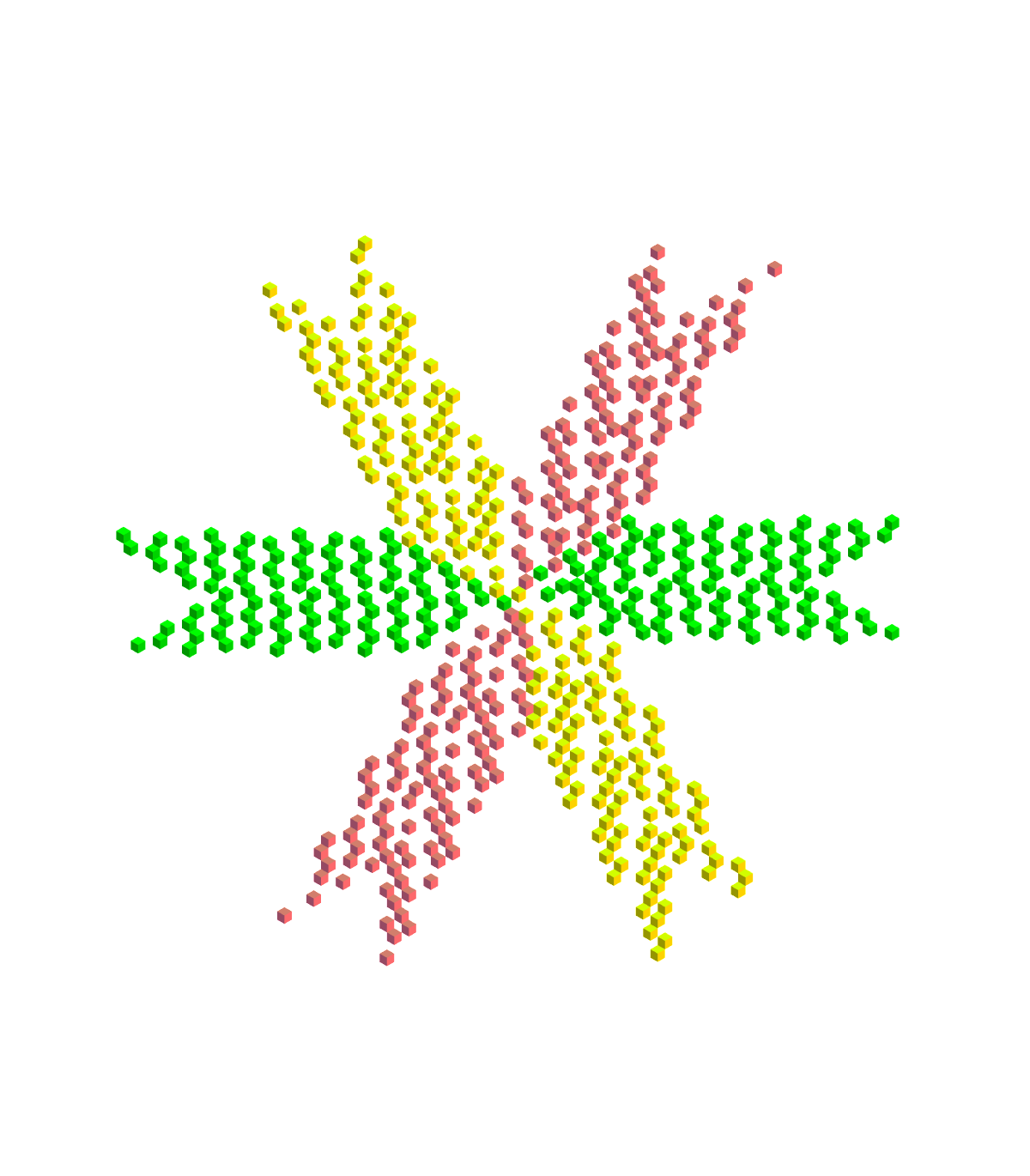
Closed to the back:

Randomly chosen bases:

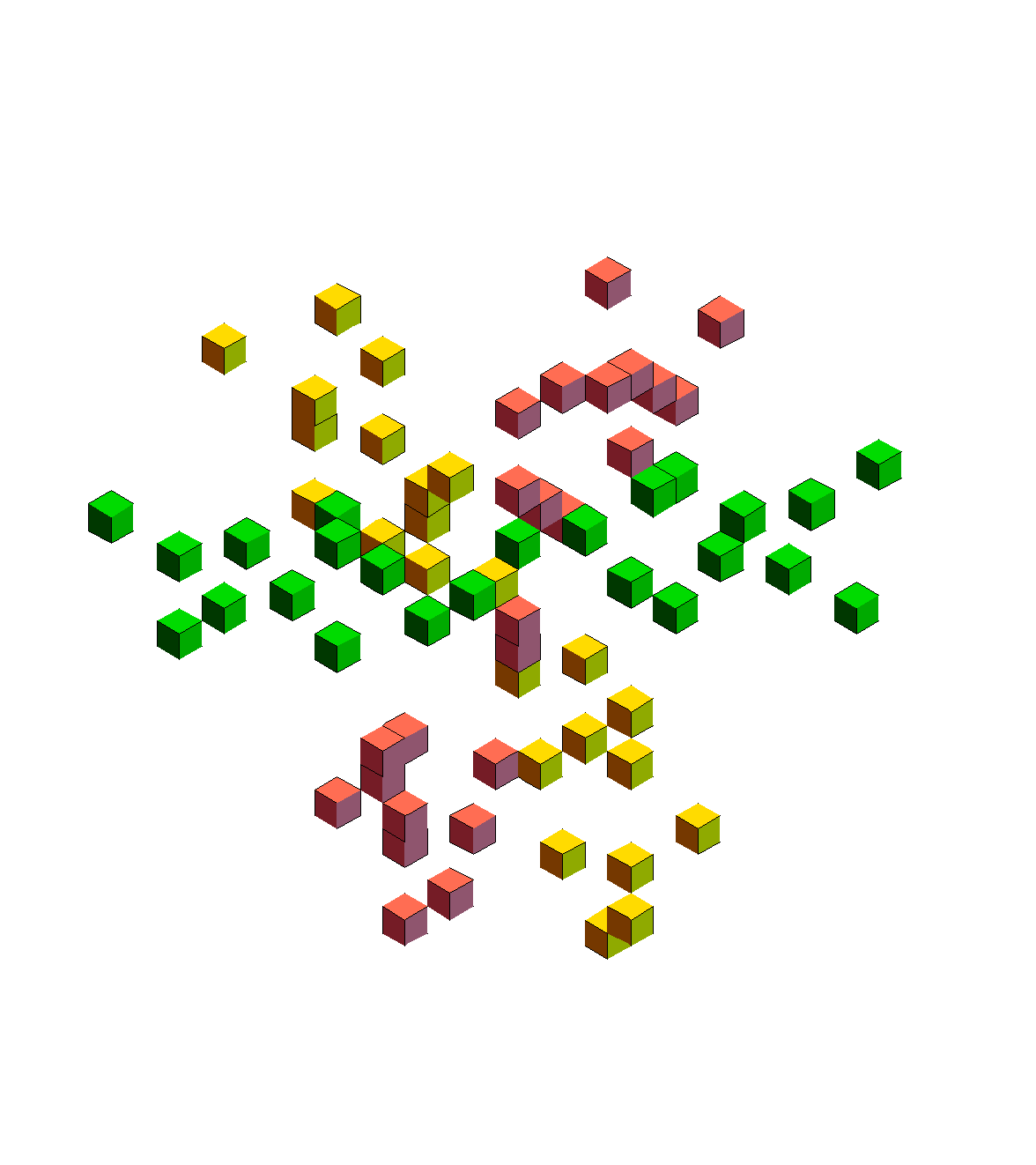
Puzzle 6. Choose the bases so that continuously blooming nets do not self-lacerate. This is always a challenge for me and I have gotten a bit fed up with it! In the animation above, I take the easy way out, using the opposite of continuous blooming — sequences of hinges used one at a time, which keep the foldings in their own airspace, so to speak. This way they cannot intersect, but it does not look as nice.

We might have to (or want to) cheat! There are some amusing ways to do that, of varying deviousness.

Cheat 1: Bend the rules by bending the nets:

Cheat 2: Add a front-facing plane using octahedral nets! This might help to turn the corner, since these change the directions of things. Since we'll be folding things up into cubes that project as hexagons, we could permit some of those, as well.

Cheat 3: Delete (please, at most one!) pendant face from a cube net (or octahedral net). There are 8 distinct "open top" cube nets (these are pentominoes) and 9 such octahedral nets (7-iamonds). At least this would keep things in the family.

Ghee Beom Kim's brilliant figure is what made me wonder about all this, namely, to find some kind of stepped figure composed entirely of cube nets. I have only done it with net #8 after trying to get more crazy. If such a thing is possible as his figure (loads of steps), using only cube nets, that would be spectacular. My crude attempts got me stuck, but there are some clever people out there who will be more successful or who will understand if it is impossible.

Notice that in his creation, each shape that appears normal to a particular coordinate axis is surrounded by figures appearing normal to the other two axes. That doesn't seem necessary, but is a neat artistic choice.

Here is, however, a perverse thought: Each of the pieces in his image is not only a polyomino, but also a subset of that very same cube net! So we could just fold up what is there! Maybe later...