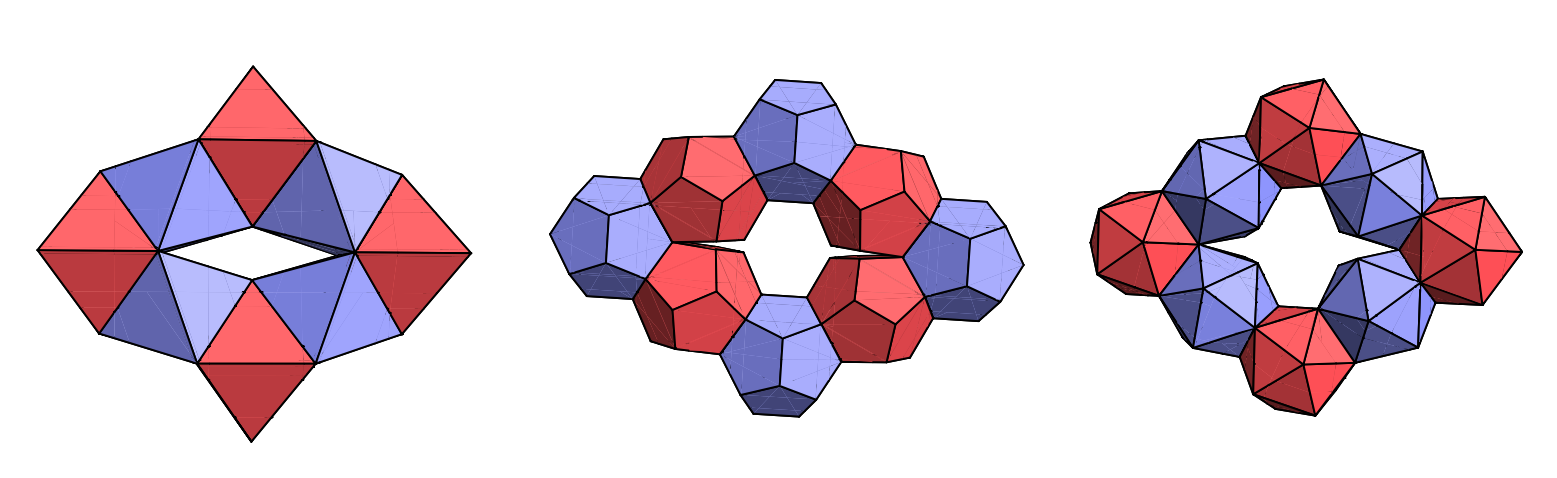
There are chains of octahedra and chains of icosahedra that meet end-to-end to form a ring, amounting to a toroidal (or genus-one) deltahedron. Here is Figure 1 in a paper by Michael Elgersma and Stan Wagon, The Quadrahelix: A Nearly Perfect Loop of Tetrahedra [new window; arxiv.org], showing deltahedral torids with 48 (the 8 octahedra) and 144 (the 8 icosahedra) triangular faces.
John Horton Conway created a toroidal deltahedron with fewer triangular faces than required by those above. He said so on the thread here [Google Groups; opens in new window]. In that same thread, Heidi Burgiel gave a simple description of the result (thank you Heidi!) that I have used to construct the beast. The result is below. Click the play button and you'll be taken through the steps that Heidi listed (which I have quoted after the video).
JHC claimed, without proof (but surely without refutation), that the number of faces he used —36— was the minimum possible:
"Martin Gardner asked for the smallest number of equal equilateral
triangles that can be used to make an embedded torus, giving some
answer that I improved to 36 (if I've just counted them correctly
from the model I have here). I'm sure 36 is smallest, and uniquely so.
"Start with an octahedron with one face up and one face down. It will
have six "side" faces. Fit three more octahedra face to face with
three of these side faces (equally spaced, of course). Looking down
on the object, you should see three square-pyramidal shapes pointing
up and away from the central octahedron.
"Place tetrahedra face-to-face with the other three side faces of the
central octaedron, and pack the spaces between the outer octahedra and
the tetrahedra with six more tetrahedra. Remove the central
octahedron (I guess you have to drill it out, or partially dissasemble
your model at this point) and you have a torus! It rests nicely on
the exposed faces of the first three tetrahedra, with the three
pyramidal octahedron peaks pointing up and out."