There are (*) exactly twelve ways to tile the icosahedron, up to congruence, using five edge-bent 4-iamonds (tetriamonds); all 12 tilings are shown further ahead. You can rotate and examine the examples.

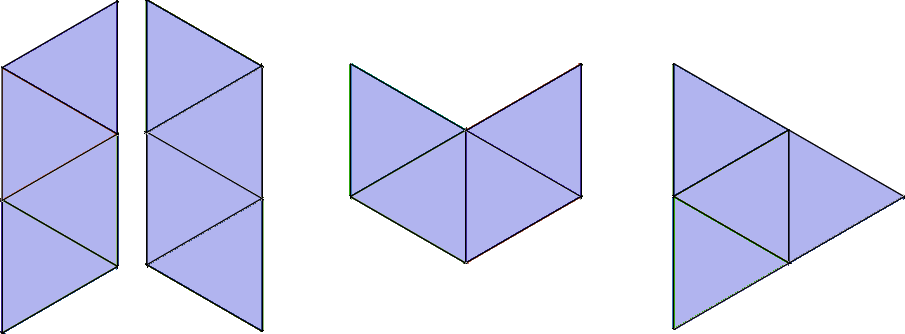
The set of 4-iamonds (tetriamonds) is shown just below. (Why don't the 4-iamonds or 5-iamonds have individual names, like the hexiamonds? Mathworld We'll just call them the two parallelograms, a chevron, and a triangle.) There are three 4-iamonds, up to congruence, but we show the parallelogram twice, since its mirror image is different in the plane (or when placed on the icosahedron). Another way of putting it is that there are three two-sided 4-iamonds and four one-sided ones.

The lists of four numbers shown in each of the 12 cases below simply indicates how many of each type appears in each tiling, the first two are for the pair of parallelograms and are grouped in arbitrary order, then the counts for the chevron and triangle. The total number of nets containing those shapes are given (*), as well; each folds to the same object.

Below, I've chosen nets that I think do a reasonable job of representing the tiling and showing off the different pieces. Maybe you'd like different ones! Then click the "PDF" link and a new window (or tab) will open with a very long, one-page PDF of all the nets for the given set of tetriamonds. (My Firefox browser (version 107.0.1) makes a blurry mess of the longest lists; Chrome works fine, as well as the PDF viewer on my laptop. Let me know what you experience. [RMABRY squiggle LSUS dot edu].)

1 of 12 ({5, 0}, 0, 0) 45 nets PDF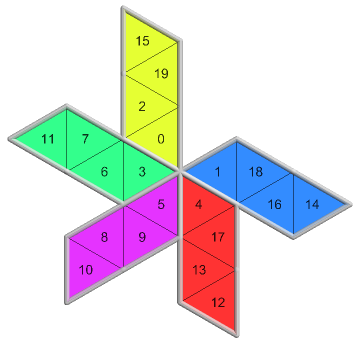	2 of 12 ({3, 2}, 0, 0) 243 nets PDF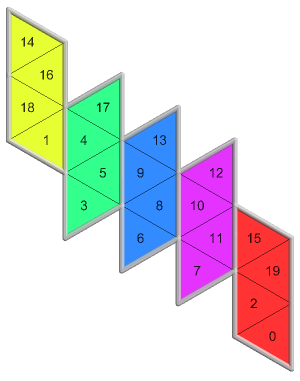	3 of 12 ({3, 0}, 2, 0) 787 nets PDF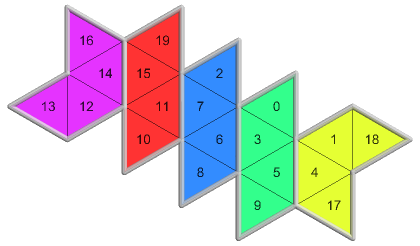
4 of 12 ({2, 1}, 2, 0) 1335 nets PDF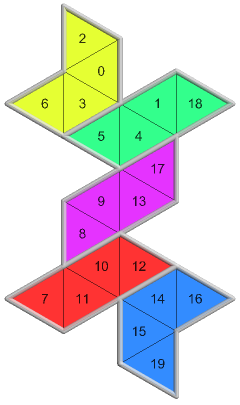	5 of 12 ({2, 1}, 1, 1) 544 nets PDF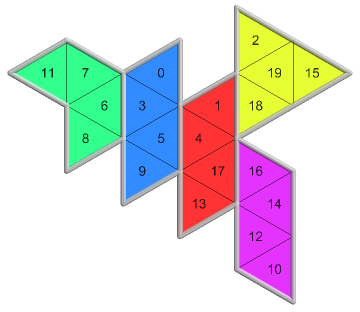	6 of 12 ({3, 0}, 1, 1) 544 nets PDF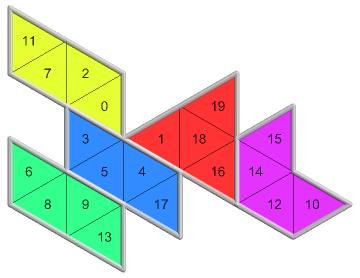
7 of 12 ({1, 0}, 3, 1) 1088 nets PDF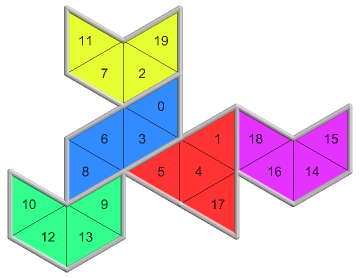	8 of 12 ({1, 0}, 2, 2) 301 nets PDF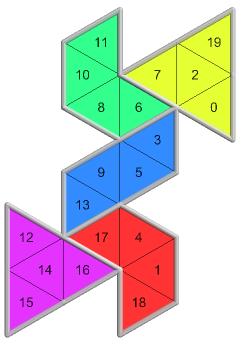	9 of 12 ({4, 1}, 0, 0) 273 nets PDF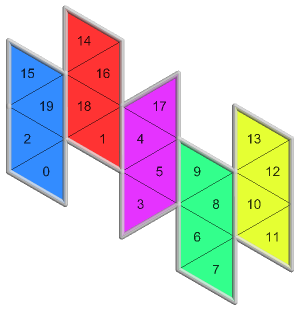
10 of 12 ({1, 0}, 4, 0) 1078 nets PDF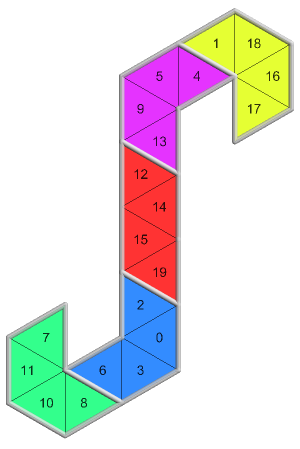	11 of 12 ({0, 0}, 3, 2) 98 nets PDF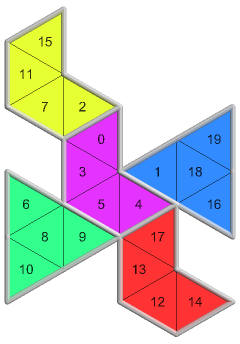	12 of 12 ({3, 0}, 0, 2) 105 nets PDF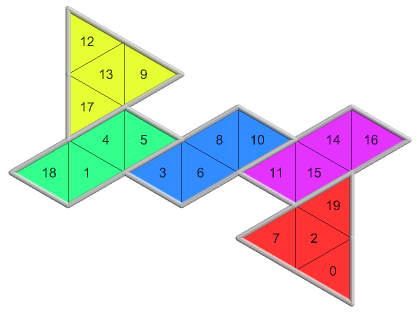

It is well known that there are distinct 43380 nets of the icosahedron, up to congruence. So the number of nets that tile the icos and that are themselves tiled by the tetriamonds comprise of 45+243+787+1335+544+544+1088+301+273+1078+98+105=6441 of those(*), or just over one-seventh of the 43380.

(*) Everything here is based on my own computations, circa December 2022. These claims should be considered to be conjectures or opinions (or utter nonsense) until confirmed or proved by someone else.

Caveat and credit: The rendering of the closed figures is done using the following, JerryI/Mathematica-ThreeJS-graphics-enginegithub (downloaded to my own site and slightly modified), which in turn uses a very outdated version (r116) of three.js, a copy of which is locally stored on my site. All of this is evident in the page source. Unfortunately, the rotation of the icosahedra can be quite annoying, as it gets "stuck" in some orientations.