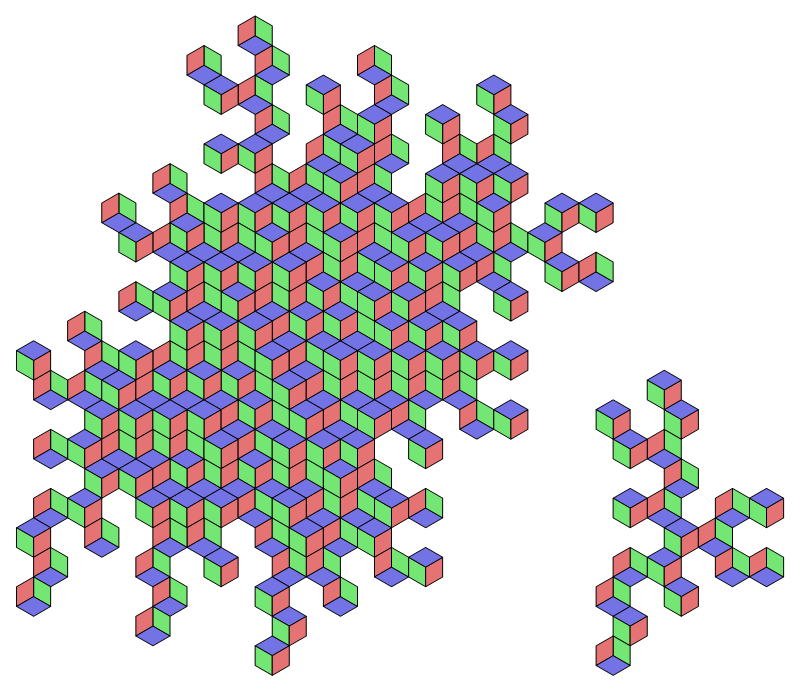
The image above (inspired in part by Ghee Beom Kim on the Mathematical Tiling and Tessellation Facebook group) is best understood in stages. It's a tiling of a truncated net of an icosahedron.

It begins with this net of the icosahedron (no. 642 in my list), one that tiles the plane using only translations:

We truncate the net. Here it is with some support...

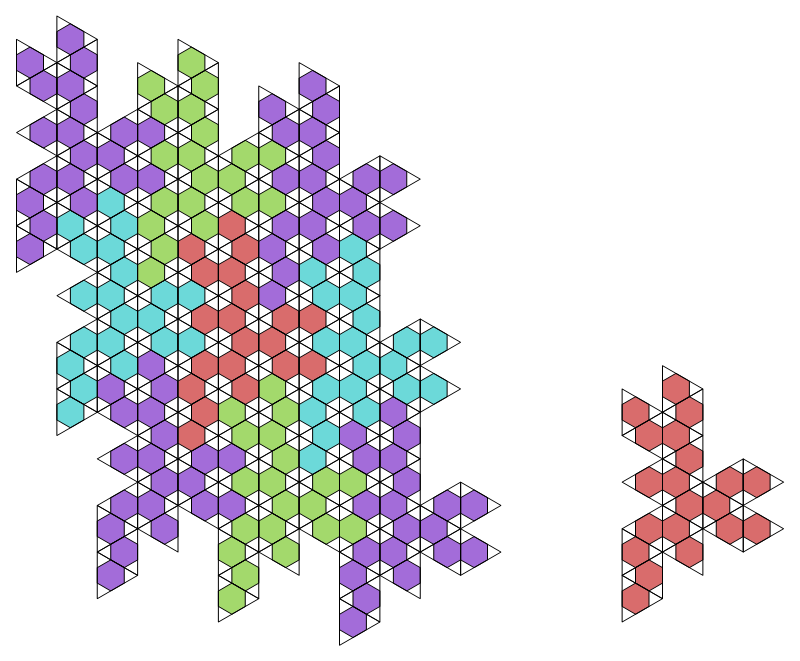
... here without, as a "polyhex":

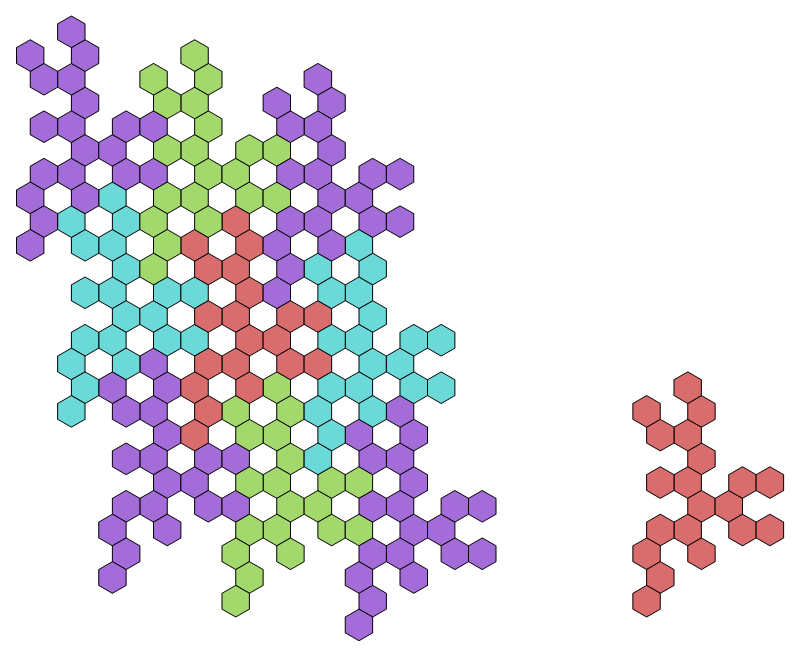
What's cool is that the truncated net by itself also tiles:

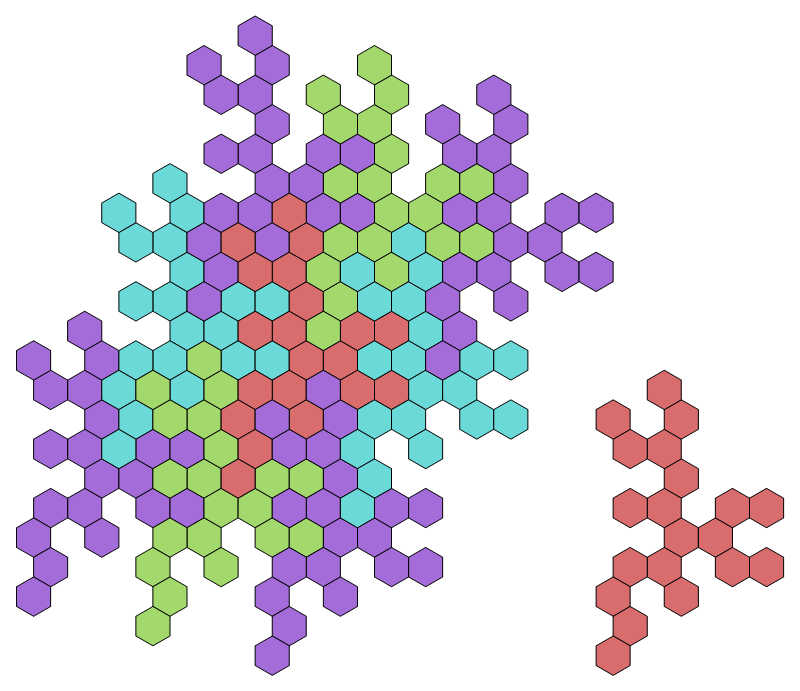
That is not true in general. Here is a different icos net that tiles (no. 27893 in my list).

But (as far as I can tell, at least using translations) the truncated version does not tile. (I'll be embarrassed if I'm wrong about that, but let me know if you learn otherwise.)

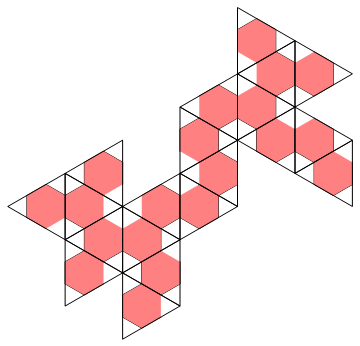
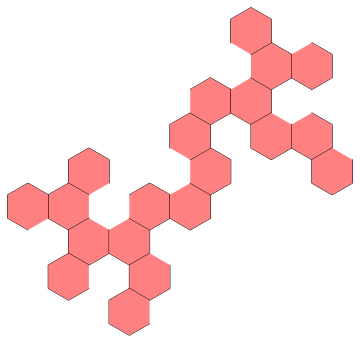
The following follows the two different tilings.

All this folderol is for one particular icos net, and there are surely many others to fiddle with. Thus — naturally! — it must be determined exactly which of the 43380 truncated icos nets tile the plane. I'll update this page when I know.

For now we're just having fun. One thing we must do is see the truncated icosahedron by folding up the truncated net:

There was some earlier fun with this same net. The following is related — it's the flappin' version of the image at the top of the page:

This is easier to comprehend:

This is just silly, but the rhomb orientations are chosen at random anyway (to avoid trying to find something artistic or interesting), so here is a repeating sequence of 10 different random choices, displayed at 6 seconds each. What would you prefer?