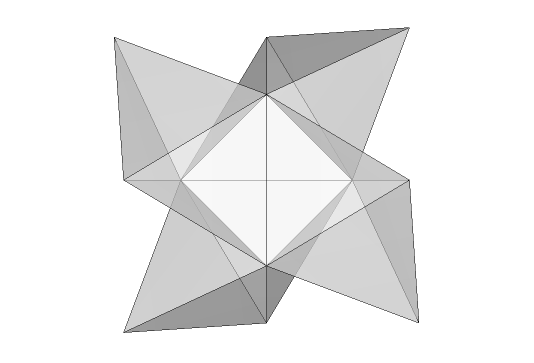
The images below illustrate the smallest polytet (a 9-tet) having no chirality but having no bilateral symmetry, i.e., no plane of symmetry. This property is made clear in the first animation — the critter's achirality is shown via a proper rotation to its faux mirror image, shown at the first pause, where the orientation and viewpoint (and lighting) show its left-right symmetry. The animation continues indefinitely, but you can pause it yourself for easier inspection.

A colored and labeled version makes it easier to track the movement.

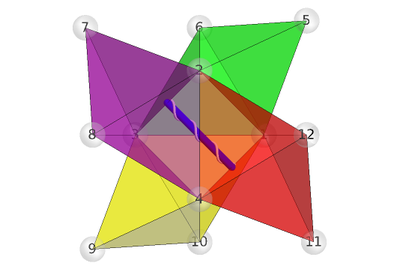
It's cool that the inner tetrahedron is discernible through the translucent triangles, where we see the axis of rotation (and the turning of the screw). That axis is through the midpoints of the two opposite pairs of the "inner" tetrahedron's edges labeled {1,4} and {2,3}, and also passes through the centroid of the inner tet (which is also the centroid of the polytet). A turn of 180° through this axis results in the faux mirror image that we see from the chosen viewpoint. That viewpoint is along the line containing the midpoints of the other pair of the inner tet's edges, labeled {1,2} and {3,4}.

What is interesting, or at least amusing, is that a rotation of 180° about this second axis (the line of sight) results in no change (other than to the labels and colors). That is also true for 90° and 270° rotations about the second axis. This is clear from just looking at the static image (above, left), since as a 2-dimensional figure it has 90°-rotational symmetry. So what happens with 90° and 270° rotations about the screw? We should get two images that also faux mirror images, right? You can pause the video above to get an idea of these, but here they are for easier close inspection:

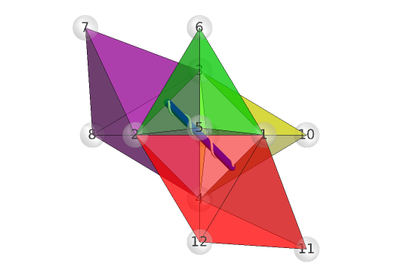
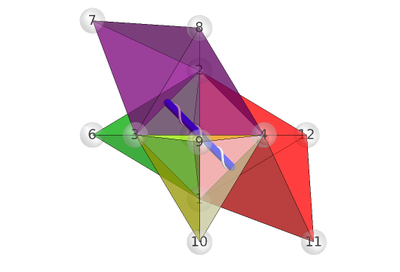
But no, those two images above are not mirror images, even when the labels and colors are removed, one being a 180° rotation of the other (aside from colors and labels) along our line of sight. My intuition fails me here. These rotations are making my head spin.

Here's the inner tetrahedron undergoing the same transformations and from the same viewpoint (screw not shown). This shows the even parity of the proper rotation through half of a revolution — the pairs "RY" and "GP" of the tet each get transposed. (The letters G,R,Y,P stand for the colors of the opposite faces.) Thanks to George Sicherman for pointing this out to me.

Gerge Sicherman also informed me of a polycube example. Below is a 10-cube due to W.F. Lunnon (cited at the bottom), which is another example of "an achiral 3D object without central symmetry or a plane of symmetry" (see this Wikipedia page for their example of such a figure). The 9-tet above and this 10-cube are the examples of that phenomenon having the minimum number of tets or cubes (or faces or vertices) in the respective classes of polytets and polycubes. The Wikipedia example can be symmetrically shortened to a 15-cube and then further to Lunnen's 10-cube.

George Sicherman also informs me that with polycubes, all centrally symmetric cases are also achiral. The example below is Lunnon's 6-cube that is achiral without having a plane of symmetry and has the least number of cubes for that. For comparison, there are no centrally symmetric polytets.

W.F. Lunnon, Counting Hexagonal and Triangular Polyominoes, Graph Theory and Computing (1972), 87–100.