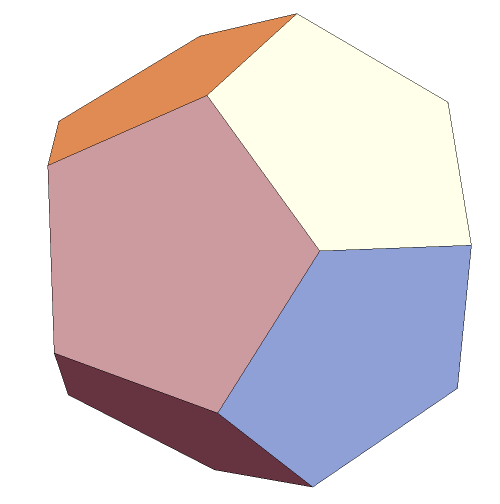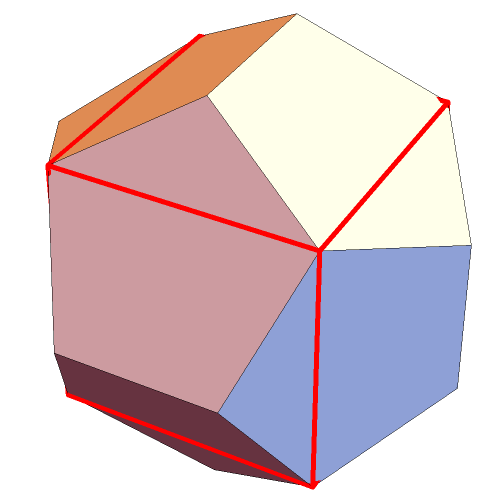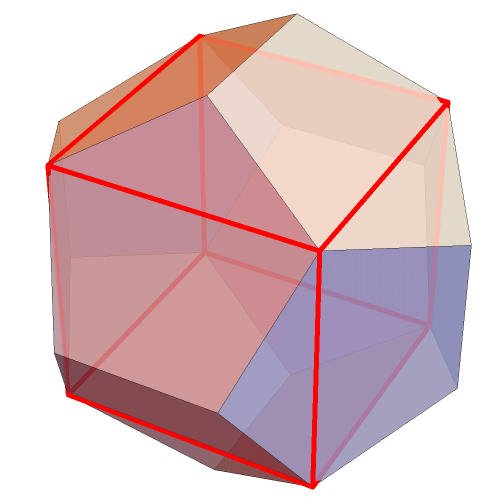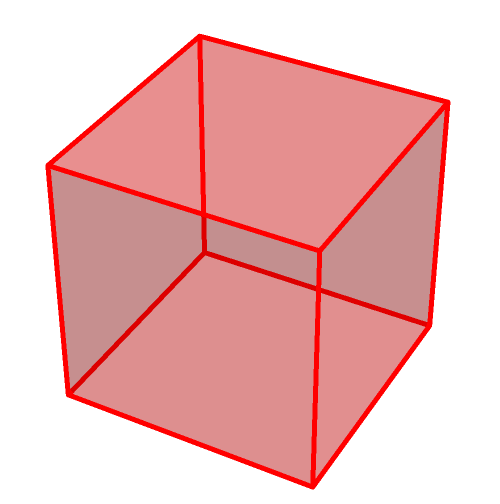
After you play the video below and after you agree with me that the twelve dancing figures are just cuter than heck, I'll try to explain what is going on.
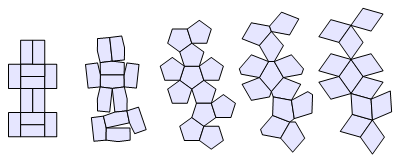
The twelve figures above are clearly distinct except when the pentagons become rectangular. I'll come back to "The Twelve" and its relatives later on.
Next is "The Five". (The names are only for future reference.) This time you see a certain selection of five animated figures. These are nets of pyritohedra being folded up, the pyritohedra being the folded-up "solid" forms. The parameters used in the sequence (as well as in the video above) include the one for which the pyritohedron corresponds to a regular (Platonic) dodecahedron, whose faces are regular pentagons. (Thus we can also call the regular dodecahedron the regular pyritohedron.) In the case of "The Five", the nets coincide in the regular case, as opposed to the rectangular case with "The Twelve". The animation pauses for you to admire that, but you can pause it at any time. Pyritodohedra are described here Wikipedia; an animation of the changing parameters is here Wikipedia and I also include such an animation below. The faces of any pyritohedron are pentagons that are bilaterally symmetric, but not (in general) regular.
Let's call a pyritohedron "proper" if it is not concave (as in this [animated gif]) and if it is not one of the three forms at which the video below pauses. We'll call the first of those paused cases "rectangular", for obvious reasons. The second is the regular dodecahedron. And the third we'll call "rhombic", since the pentagons degenerate to rhombi. The third figure is also known separately as the Rhombic Dodecahedron Wikipedia. I chose not to include that form in the animations above, since the degenerate edges don't make such visual sense for a net. But I'll show an example later below.
I calculate (*) that there are 216180 nonisomorphic (i.e., geometrically distinct) nets of any given proper pyritohedron. Comparing that with the 43880 nets of the regular dodecahedron, we note that
216810 = 5×43380 − 2×360.
As a hint about what that reveals, note that above in "The Five", there are five nets that coincide, below there are three. The trios — there are 360 such trios — correspond to those 360 nets of the regular dodec that are (point-)symmetric. In each such trio there is one symmetric net and two impostors. If you pause the video when they are laid out flat (in a nonregular mode), you can spot the symmetric one. There are thus 360 symmetric nets among the 216810 distinct ones. Evidently, for each of the 43380 nets of the regular dodec, we get five nets of any (nonregular) pyritohedron except when the dodec net is symmetric, in which case two pairs of the five consist of congruent nets (thanks to the bilateral symmetry of the pentagons forming the pyritohedra).
Regarding the rhombic cases, there are, however, 13824 nets among the entire collection of 216180, for which those degenerate edges are not involved. So it is hard to object to those cases on visual grounds! One of them is shown in the next animation, surrounded by its four objectionable siblings. If you pause during the folded-out rhombic phase, you'll see how the poor things are hanging together only by threads.
As I said, 13824 nets in the collection of 216180 do not involve degenerate edges. They fold up to rhombic dodecahedra. And did you know that there are 6912 nets of the rhombic dodec? And do you notice that 13824 = 2×6912? What the heck?
A word about "The Twelve" in the first video on this page: Clearly those 12 nets are related by the congruence of the rectangular forms. If you sort the entire collection of 216180 nets into families that have congruent rectangular forms, you obtain 5012 such families. "The Twelve" were selected for viewing because 12 is a smallish number, so the family could be viewed together without the individual critters having to be made too small. There is just one family of size 12 — see the tally of all sizes of such families below and note the entry {12,1}.
{{1,309},{3,554},{5,24},{6,6},{8,785},{9,517},{12,1},{24,1092},{27,282},{32,5},{36,8},{39,15},{44,1},{45,2},{64,318},{72,601},{81,86},{96,4},{132,1},{192,207},{204,2},{216,130},{243,9},{256,3},{264,4},{288,2},{300,1},{333,1},{432,2},{435,1},{459,2},{512,7},{576,25},{648,4},{768,1}}
The tally shows that there are 309 cases whose rectangular forms are unique and there is a family consisting of 768 members whose rectangular forms coincide. Here is one of those 768 members.
Of course, since the rectangular form of the pyritohedron is a "cube" (with all the sides split in two), there are certainly nets of the rectangular pyritohedron that fold out to resemble each of the 11 nets of the usual (regular; Platonic) cube. These are shown below.
What's with the spots? They make for some very boring dominoes. They're there for fun, but I actually used their positions to confirm that there are no face-overlaps when the rectangular forms are folded flat. So these "nets" are indeed nets in that sense. However, there are plenty of edge overlaps and vertex overlaps, so maybe some purists would object. (We note that the net-connected edges are not distinguishable in the above cases; more about that further ahead.) I gathered the lengths (each rectangle as 2×1) of the resulting perimeters of the rectangular unfoldings to get a sense of how crowded the different members of those 5012 families are. Here are the results, given as {perimeter, number of corresponding rectangular pyrito-nets}:
{{28, 26}, {30, 92}, {32, 241}, {34, 418}, {36, 623}, {38, 740}, {40, 854}, {42, 608}, {44, 671}, {46, 430}, {48, 53}, {50, 256}}
The most crowded cases have perimeter=28 and there are 26 of those, below.

Anyway, those spot positions should not go to waste, so I made these dicey pictures. Below are the 11 that I was hunting for, culled from the most-crowded 26.

Above, the number of unique nets is shown with each of the 11 cube-net replicas. The number 243 stands out, since 243 = 35. And indeed that can be verified straightforwardly: at each of the 5 meetings of the "squares" of that particular "cube net" (called "Wb", says Kate gamepuzzles.com), there are three possible ways to connect the faces to form the actual rectangular pyritohedral net, as shown at one such meeting with the following crude markings.
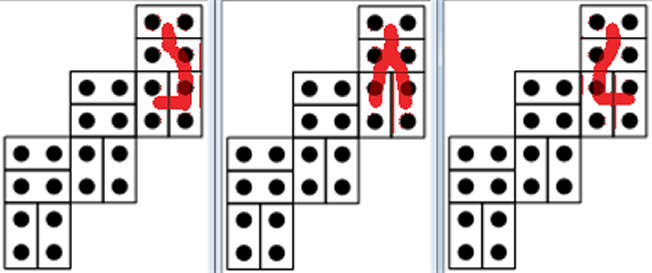
I verified the counts of 204 and 216, as well. The exercise is not difficult and was even more interesting than I suspected it would be.
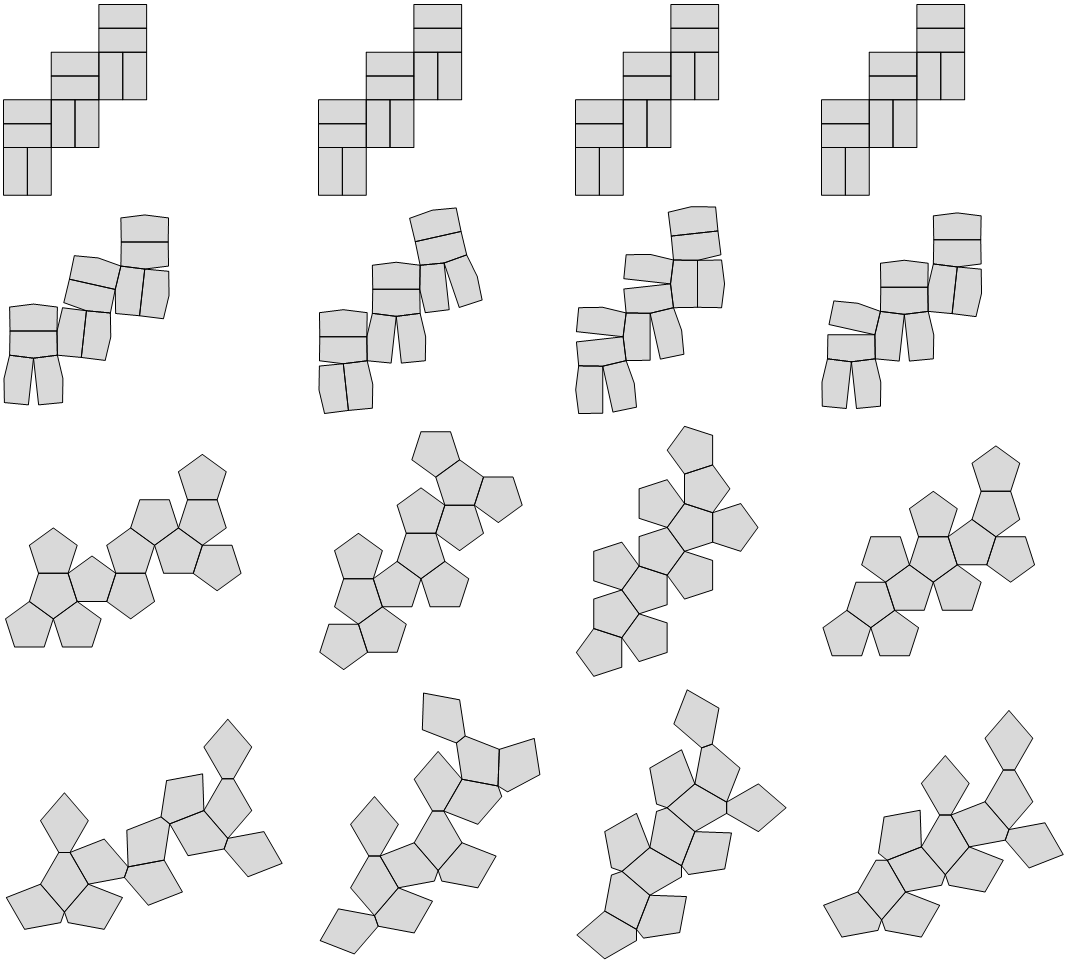
Below are 4 of the 243 Wb-nets in various forms.
I do not know how to prove that all 216810 of the other convex-faced are indeed bona-fide nets, i.e., non-overlapping when folded flat, but I conjecture that they are. By that I mean a proof for all of the continuum of forms — from not-quite-rectangular through regular to almost-rhombic. It is known that the 43380 regular ones are so — see the paper by Horiyama and Shoji (2011), Edge Unfoldings of Platonic Solids Never Overlap ResearchGate. The tricks there are applicable to the general convex cases, but only on a case-by-case basis, i.e., for each parameter (rectangular through rhombic). The trouble remains, even with that paper, that the verification is done separately, a geometric test is applied to each of the 43380 cases. There seems to be no known "synthetic" proof for this result!
The concave versions can be a mess, as you'd expect, with plenty of overlapping, but some can be nets. The messiest ones have the most "T" joins in the rectangular form. I'll leave that notion undefined, but it is easy to identify the ones that do and do not admit nonconvex nets (i.e., unfoldings that do not have face overlaps). It makes sense that in the perimeter list shown previously, the maximal perimeters produce concave-admitting nets. (I say "admitting" because when the parameter becomes sufficiently extreme, the faces can overlap.)
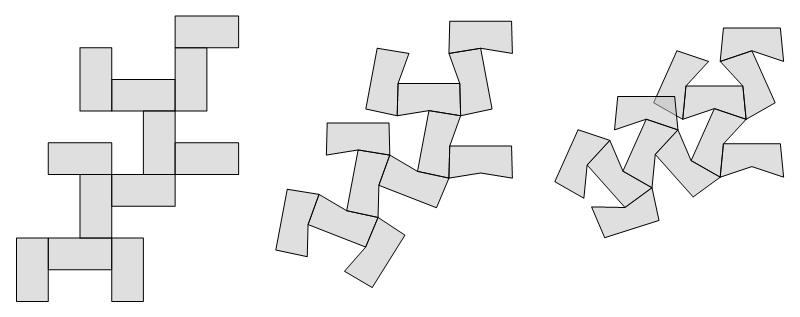
The rectangular forms with perimeter=50 or 48 give rise to just one net apiece and those allow for concave nets. The ones with perimeter=46 each come in three forms, none of which admit concavity, like so:
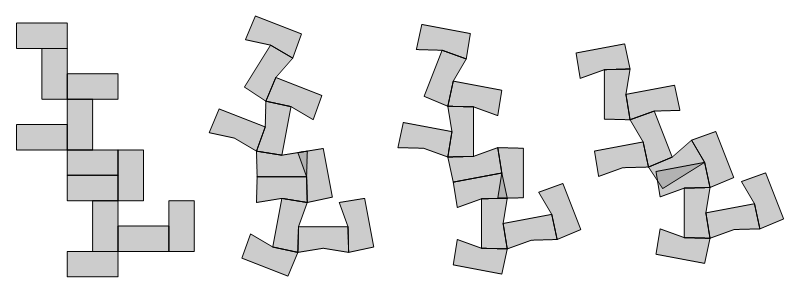
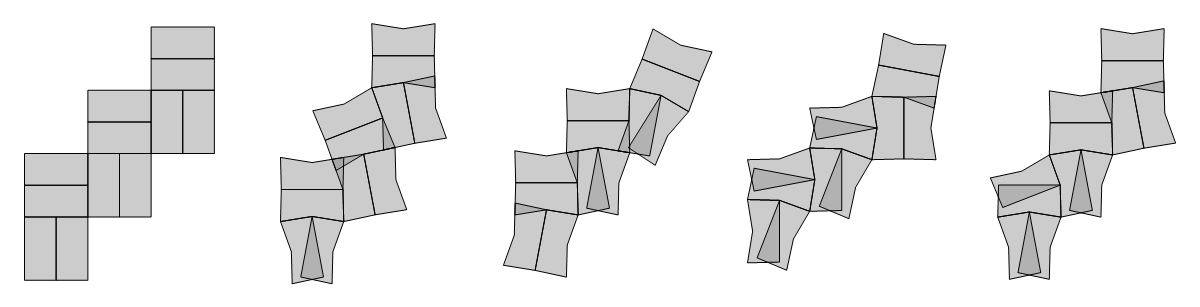
I haven't checked or thought about it throughly, but I suspect that when the perimeter is less than 48, then concave nets do not occur. Here is what happens with the four (out of 243) "Wb" examples we saw earlier:
I'm way too amused that there is a cube within a dodecahedron. Always striving to be the last to know, I only just became aware of it. But it is obvious that there's a cube in there.
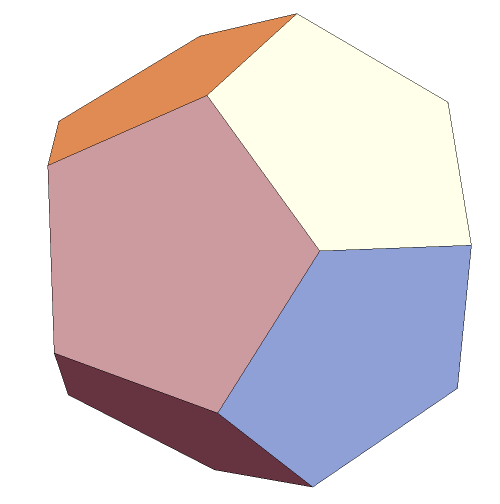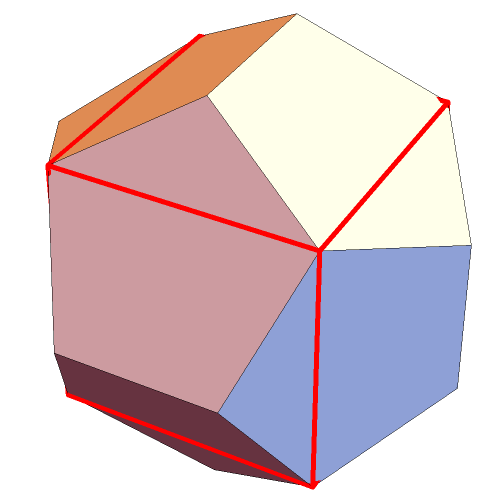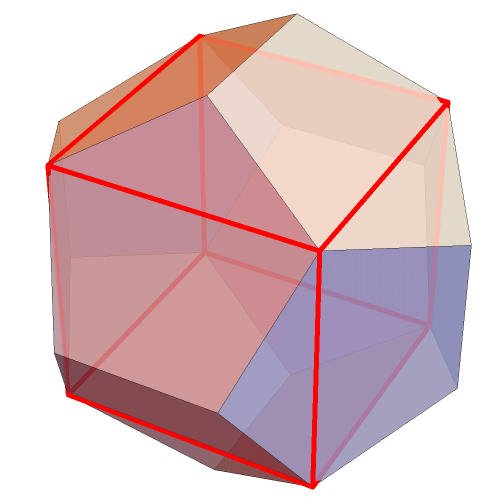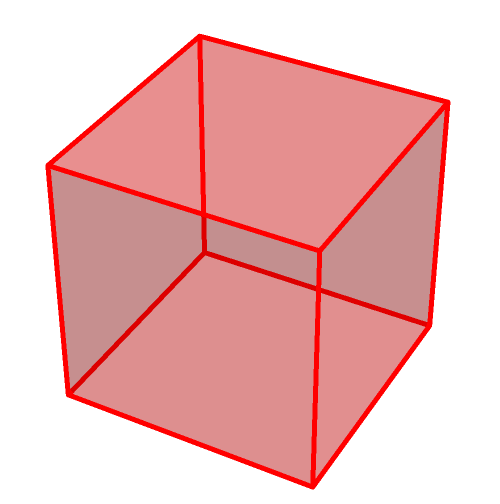
Actually, there must then be five such cubes. This is well known (and I was the last to know that, too, unless you also did not know).
The cube is the source for all the pyritohedra; it is evident from the first image. Included below are even some of the wilder versions with nonsimple faces:
There are 5184000 labeled nets of the pyritohedron (and regular dodec and regular icosahedron).
I used the method described in [HS] to calculate the number of these that should be distinct, based on the symmetries of the pyritohedron: 216810. This was in some ways an exercise, but it was a valuable one, since I had never thoroughly studied it. But that doesn't get me the whole collection, so I ground those out by generating all 5184000 labeled versions, then sifted those via symmetries. With only 5184000 cases, this doesn't take forever (just a few hours). And there were indeed 216810 unique nets.
[HS] Springer T. Horiyama and W. Shoji (2013), The Number of Different Unfoldings of Polyhedra.