Below is a slight modification of the earlier Flapping Snub Dodecahedron (version 2), modified to cause a collision when the flaps are completely unfolded. This situation is mentioned in Croft, Falconer, and Guy's Unsolved Problems in Geometry: "We can get an overlapping net if we cut perversely."
Actually it didn't take much cutting; you be the judge of its perverseness. (I'd say it's just scratching itself, nothing more.) Clearly much more overlapping can be had. It would be fun to find the net with the greatest fractional area of overlap. Are there any such nets that triply overlap?
Here are the two nets side by side.
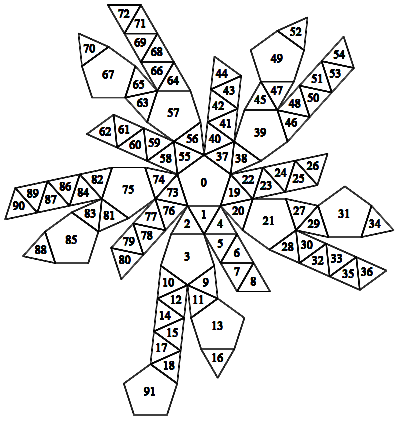
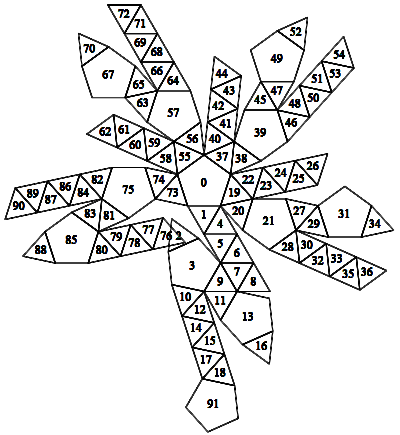
Grab it, turn it, spin it with the mouse. Double click the figure to stop the animation. You can hold the RIGHT mouse button down and drag it HORIZONTALLY across the frame to sequence through the frames.(Please be patient while the applet processes mucho compressed data.)
 .
.