Mathematics and geometry feature prominently in the game of pool. Recently a clever guy named Rick Mabry figured out something interesting about the game using mathematics and trigonometry. His work was published in a minor scientific journal as reported in New Scientist. It’s actually a bit surprising, somewhat useful to players, and even a bit magical in some sense.
Update: after some added diligence I located the full paper online here and reviewed it. I’m not competent enough to question the math. That seems correct to the degree I can verify. But I do question the result. I’ll leave my summary of the paper intact for now and include my counter-argument at the end of this post.
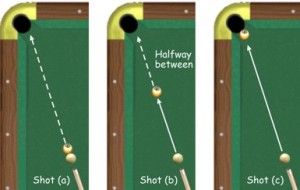Most
casual players assume that the easiest pool shot is a straight-in shot.
Fair enough. The straight-in shot eliminates the judgment involved in
deciding how to aim cut shots. But not all straight-in shots are the
same. The object ball can be located right next to the cue ball, shot
(a), right next to the pocket, shot (c), or anywhere in between. Rick
Mabry used some basic trigonometry and math to determine which of these
shots was hardest and easiest.
If you assume you can shoot the cue ball with perfect accuracy like a laser, the result is simple and wouldn’t surprise any pool player. The easiest straight-in shots are when the cueball and object balls are closest together, shot (a), and when the object ball is closest to the pocket, shot (c). The hardest shot is when the object ball is halfway between, shot (b). This result is so obvious that it’s hardly worth the effort to prove. But there’s more.
Rick Mabry didn’t think that was a very interesting result either, so he tried a more realistic analysis. He extended his calculations for a shooter who is not perfectly accurate. This affected the result, and in an amazing way.
Mabry’s calculations show that when a player’s accuracy is low, in this case meaning that the cueball will hit the object ball but not necessarily where he or she wants, the difficulty of the shot is greatest when the distance from the cueball to the pocket is 1.618 times the distance from the object ball to the pocket.
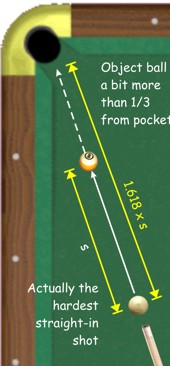At
first glance 1.618 seems like an odd result, and not one that a pool
player would ever come up with on their own. But in fact, it’s a very
famous and interesting number. The actual value is (1+sqrt(5))/2 or
1.6180339887… which is well known as the Golden Ratio.
The Golden Ratio is found throughout nature in sea shells, flowers, and
crystals. It’s been used by painters, architects, and musicians for
ages to achieve proper aesthetics. Now we find, it’s integral to the
game of pool.
We can use this new knowledge in a few ways. First, when we have ball in hand, especially with the cueball in the kitchen, we can know NOT to position the cueball from the object ball by this ratio, otherwise we’ll be unnecessarily making the shot too hard. Another more clever use is when playing a safety. There could be situations where we intentionally leave this hardest straight-in shot rather than something easier. And finally we come to bar bets. We could bet a player that they couldn’t make as many shots from this position as from the midway position. Given enough shots, we’d be sure to win our bet! I’ll have to put that to the test before recommending it for real.
Further consideration
I wrote the above summary based on information I gleaned from the article in New Scientist. Such summaries of published papers are often wrong or include misinterpretations of the research. I located a copy of Mabry’s paper online, reviewed it directly, and tested the conclusions on a pool table. Then I used my own math skills and more formidable computer skills to test the results. Unfortunately my conclusions were different. I don’t feel like I have a firm enough grasp of Mabry’s paper to point out exactly what’s wrong, but I’m confident in my own results so I’ll share them.
First I rushed out to do some experimentation. I have some credentials in pool having played competitively for over 20 years at a respectably high level. I shot a few hundred straight-in shots on a regulation table. It’s a practice drill I’m well-acquainted with. Straight-in shots may be considered the easiest, but in fact they exacerbate the slightest errors in alignment and cuing, moreso than any other shot. I soon got a feeling of certainty that the midway shot was the toughest. If anything, placing the object ball further from the cueball, made the shot harder while moving the object ball closer to the Golden Ratio point made the shot a bit easier. It wasn’t a scientific experiment, but it was clear enough to motivate me to delve into the math.
I found the original article and read it. It was confusing. The math was mostly simple (at least the trig, my calculus is long gone). But Mabry’s definition of difficulty was a bit confusing and his discussion of some of his techniques confounded me. The main issue I had was understanding what the difference was between his two cases (1) a shooter who was perfectly accurate and (2) a really bad shooter.
My analysis is more straight-forward, and I think easier to explain and justify.
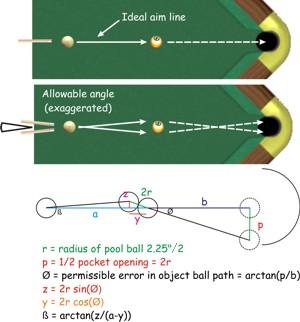
First I’ll define shot difficulty in a way that I think is more standard and quite a bit easier to understand and work with. Ignoring subtleties like spin, throw, cloth, balls, humidity, and so on, and sticking solely to the geometry as Mabry does, I define the difficulty of a shot as being directly related to the greatest permissible difference in angle that you can strike the cueball and still make the shot. An easy shot is one in which you can hit the cueball at a largely incorrect angle relative to the true aim line and still pocket the ball. A hard shot is one that you can only be off by a hair. For any shot you can lay out, there’s an ideal aim line. If you deliver the cueball along this line, the object ball will be sunk in the center of the pocket. And each shot has what I’ll call an “error angle” in each direction. If the error angle is one degree, you can strike the cueball in the wrong direction by as much as one degree and still make the shot. Thus if the error angle is greater, say two degrees rather than one, it’s an easier shot.
Now the math becomes fairly easy, just some basic high school trig:
My calculus is rusty so rather than deriving a formula for the a-to-b ratio that results in the hardest shot (meaning smallest error angle ß), I instead used a spreadsheet. I kept the full distance a+b constant at 60″ and varied a and b. At the midpoint a=30, b=30, ß=0.347 degrees. Surprisingly, the hardest shot was not at a=b, not at (a+b)/b=1.618, not even a < b, but rather it was about an inch and a quarter nearer the pocket than a=b. That small offset has to do with the geometry of the collision. But the logical conclusion, to a practical estimate, is that the hardest straight-in shot is really about midway between the cueball and the pocket. And it seems to agree with experience.
Hi John,
Nice blog! And I do not disagree with anything you’ve said, though I think we need to clear up something with this combination: “I soon got a feeling of certainty that the midway shot was the toughest. If anything, placing the object ball further from the cueball, made the shot harder…” I assume you mean further from the cueball than halfway. And that’s just what my results say: The hardest shot (for the untalented players) occurs when the ratio T/Y is about 1.618, where T is the distance from cue to pocket and Y is the distance from cue to object. So more like this:
http://www.lsus.edu/sc/math/rmabry/pool/inaccurate-rdm.png
That should make us both closer to agreement.
Anyway, your tests and analysis concern the difficulty of actually making the shot, i.e., sinking the ball, and so you consider the size of the pocket. My version had only to do with total deflection at the target, as if the goal is to come closest to an exact spot, a mere point. Obviously that is not what practical pool players need to be concerned with.
I’d have liked to do the diligent thing — an experiment — but decided it would involve too much technology, time, or trouble. It would be cool to measure total deviations, such as those arising from shooting straight down the middle of the table to the rail, measuring/recording the point of contact with the rail of a large number of shots. (A sophisticated guy with good cameras, like Dr. Dave, could probably do this pretty easily.) I’ve been hoping people would do my due diligence for me!
There are many ways to assign difficulty (that’s the primary difficulty). There is nothing wrong with yours that I can see. I simply chose a different way.
Thanks for reading the article and looking into this! If you do any more experiments or have further thoughts, I’d love to hear about it.
Best regards,
Rick Mabry
LSUS
Hi Rick,
Thanks for contributing to the discussion. And of course great thanks for researching this topic to begin with.
And thanks yet again for pointing out that my diagram was backwards. I have corrected it. Now the object ball is properly closer than halfway to the pocket from the cueball. I hope this accurately represents your conclusion and shows correctly how the Golden Ratio applies.
I agree that there are different ways to assess the geometric difficulty of a shot. However, I assume you would agree that the real life difficulty of a shot is a constant based on the set-up of the balls (and somewhat on the minor differences in playing conditions such as humidity, cloth, how polished the balls are and so on), but mostly just based on the geometric arrangement of the balls. If anyone doubts that, you could arrange an experiment in which the shot was set up and shot thousands of times by many players of different skill levels. With enough proper data, one could simply measure how frequently the ball was made. So if you accept that there is a ‘real’ and determinable difficulty to any shot, doesn’t it make sense that any ‘valid’ way to measure that difficulty would yield the same result for a given shot?
So I’m wondering whether one or more of the ways in which we’re measuring shot difficulty is in error? ..not necessarily mathematically, but as reflects real-world shot difficulty.
I don’t believe that my introducing pocket size makes any difference, other than to allow me to work with real angles rather than differentials. i.e. couldn’t you reduce the same method to a point-sized target and retain the result (using differentials). What, if anything, would account for our disparate results then?
I’m not quite sure. I’d love to be able to introduce the fascinating and esoteric concept of the Golden Ratio (and credit you of course!) as I’m teaching pool, or just bantering with top players. But I’m still not convinced that it actual does determine the geometry of the toughest straight-in shot. I’ll keep at it, and I’ll let you know if I ever figure out exactly why our results disagree.
Keep up the great work investigating the mathematics of pool. I’m off the play right now. Can’t wait until my opponent scratches
Hi John,
The new graphic is good. My only quibble with it would be its text, “actually the hardest straight-in shot”,
which isn’t what I claim.
One other little thing: You said, “Mabry’s calculations show that when a player’s accuracy is low, [...] the difficulty of the shot is greatest when the distance from the cueball to the pocket is 1.618 times the distance from the object ball to the pocket.” That part also needs correcting in the same way as with the graphic. (To keep a reader from being confused by the changes, since I cannot edit these remarks, maybe you can apply some HTML strikeout to your text and then add the correction. This is pretty common in such cases.) Sorry for not catching that before.
Moreover, I want to emphasize that the golden ratio is only approached in a very idealized limit, as the size of the table goes to infinity (or equivalently, as the radius of the ball goes to zero). In the more “practical” longest shot I describe in the paper, though, the “hardest” ratio is still close to golden, so I’m not suggesting the limit is a bizarre consideration. But I have to stress that here I am speaking of a shot so bad that it just manages to knick the ball. Our “golden pool ratio” is the one that produces the greatest deviation from the pocket in that glancing case.
Calling it the “hardest” is the only cause of controversy here. I did that when I said that my analysis “shows that the most difficult shot for the most error-prone viable shooter occurs” when the ratio is close to this. But I had already defined my notion of difficulty (complete with caveats and hedging) and this was intended in the mathematical sense. But even so, it may have been unwise not to stress the assumptions again at that point in the article.
Most pool players, I’d wager, even pretty bad ones by your standards, have no problem hitting the target ball from any distance on the table (at least before consuming 1.618 beers [*]), and have a decent probability of sinking their ball on any straight-in shot. For such shooters, these extreme ratios near 1.6 do not apply at all; the angle of error at the stick for them (in my scenario) is very small, and a hardest shot of “about halfway” is the conclusion I reached, just as you did. (I do like to mention, though, that it is still a bit farther than the one-half mark, i.e., the situation is asymmetric.)
[*] I stole that crack from a clever comment made by “Joseph EH” on the New Scientist website. Actually, I think about 1.618 beers optimizes my shooting!
Your own measure of difficulty (which I also like) is asymmetric, but I think you didn’t push the results of the spreadsheet enough to show it. The reason it is harder to detect is that you are actually assuming a player is very close to the “perfect” player and very far from the “lousy” player. Your player has to always nail the shot to within 2 ball radii at the target/pocket. That implies that only very small angles of error at the stick are permissible. So, though it may seem counterintuitive, if you make the pockets bigger, then (and only then) does the “hardest shot” get near the golden distance. And that goes for your version of “most difficult”, as well as mine! (Try larger pocket sizes and you’ll soon strike gold. But beware there is a limit — make the pocket size big enough and you’ll always land in the pocket so long as you hit the target at all.)
By way of example, I’ll use your 60-inch shot length (I used about 83 inches in the article). For the 2-radii pocket deviation, the distance of the target ball’s center when the angle at the stick is smallest is about 0.5015 of the shot length [**], and the corresponding minimum angle at the stick is then only about 0.32 degrees. The ratio .5015 is still bigger than one-half (as it must be) but not very close to 0.618! And here is why: The angle I consider for the lousy player lets the cueball just nick the target ball at the full 60 inches; that angle is around 2.07 degrees in this case. With such a lousy angle as that, a target ball at the halfway mark would end up with a total deflection near the pocket of about 14.9 ball radii! Pretty lousy. The greatest deflection, for that same lousy angle, is about 15.4 radii, when the (near golden) ratio is about 0.614.
[**] As I did in the article, I like using the ratio of the cue-to-object distance to the cue-to-pocket distance, rather than the ratio New Scientist used (that you then adopted). I think mine is easier to think about. New Scientist probably wanted to be able to mention the usual “big” golden ratio G (about 1.618) instead of the “little” golden ration, 1/G (about 0.618), that I used. Also, I chose my coordinates to simplify calculations, with the cue ball behind the “zero” distance, so that the center of the target ball takes all relative positions 0 to 1. Otherwise you see the radius of the ball added to your nearly halfway point, as you noticed above (“that small offset”).
Again, and concisely: our seeming disagreement vanishes at the accuracy requirements you prefer. And in fact, our definitions of difficulty lead to the same results about hardest ratios!
Anyway, to directly answer your questions …
“So if you accept that there is a ‘real’ and determinable difficulty to any shot, doesn’t it make sense that any ‘valid’ way to measure that difficulty would yield the same result for a given shot?”
I guess I do not accept that there is one ‘real’ difficulty, but there might be one most players would agree upon. I do think that any reasonable definition will give our result, namely that as the shooter’s skill approaches perfection, the hardest shot approaches halfway.
“So I’m wondering whether one or more of the ways in which we’re measuring shot difficulty is in error? ..not necessarily mathematically, but as reflects real-world shot difficulty.”
I don’t think our results indicate either way is in error. We are in full agreement, even though you looked at an angle and I looked at a distance. Our geometry is the same. The only difference is that you looked only at small angles and used different endpoints than I did.
“I don’t believe that my introducing pocket size makes any difference, other than to allow me to work with real angles rather than differentials. i.e. couldn’t you reduce the same method to a point-sized target and retain the result (using differentials). What, if anything, would account for our disparate results then?”
No disparity here! But the introduction of a pocket size does make a difference. Also, I do use real angles (as opposed to differentials) for all but the 1/2 result.
Incidentally, though only a math geek like myself might be interested, when you take a pocket radius P, ball radius R, and shot length L, the hardest shot is at approximately the ratio
1/2 + (1 + 2 R/L) (P/L)^2
when R/L and P/L are “small”. (I used Taylor series and Mathematica for this.)
Cool pool!
Rick