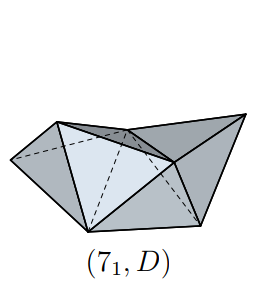
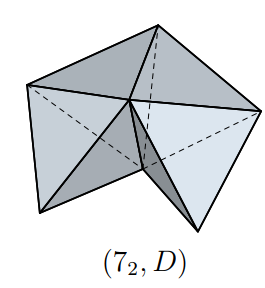
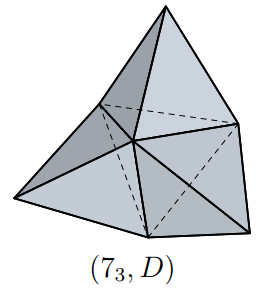
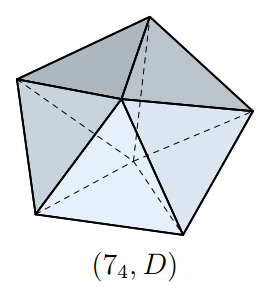
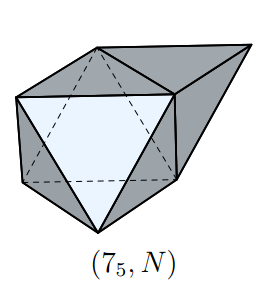
There are five 7-vertex deltahedra (if you don't count certain goofiness (*)). A deltahedron is a polyhedron whose surface consists of edge-adjoined equilateral triangles. (The 7-vertex ones therefore each have 10 such triangles apiece, which Euler's formula could have told you (**).) Deltahedra are studied in the paper [TMKF]; I've used their numbering (1 through 5) for indexing the deltahedra in what follows; here is Figure 6 in their paper:

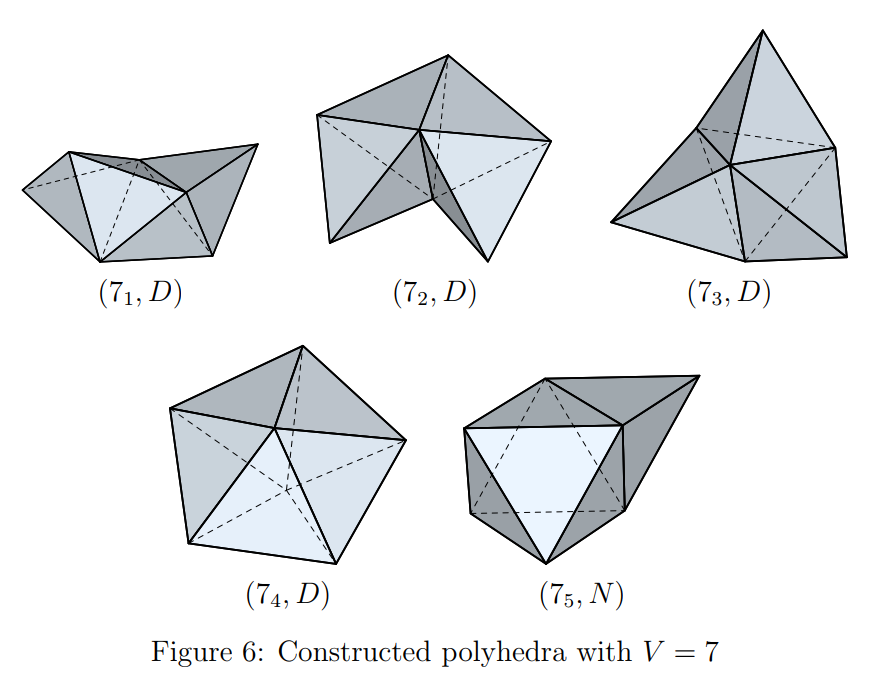
Note that I am not distinguishing between what some people call "strictly convex" deltahedra — number 4 above — or "non-convex" — these are numbers 1 through 3 above — or "non-strictly convex ones", like number 5 (where two of its adjoined faces are coplanar). The "D" and "N" notation in paper [TMKF] are essentially for "deltahedron" and "not deltahedron". The usage is far from uniform. Anyway, the term non-strictly convex strikes me as weird, since no polyhedron is strictly convex! I'll use same term, "deltahedra", for all of them, but you know the difference.

By the way, notice that numbers 1,2,3 are polytetrahedra — face-joined unions of four regular tetrahedra. (Auf Deutsch: Tetraedervierlinge.) From Wikipedia, a polytetrahedron is a "connected set of regular tetrahedra, the 3-dimensional analogue of a polyiamond. Polytetrahedra and polyiamonds are related as polycubes are related to polyominoes." That's worth noting, perhaps, since we talk about polyiamonds below. Each of these three Tetraedervierlinge is special in its own way. The first has symmetry with respect to a point — a 180° rotational symmetry. The second has two bilateral symmetries; the third is symmetric via a 120° rotation.

And notice that number 5 is a face-joined union of a regular octahedron and a regular tetrahedron. It is sometimes called an augmented octahedron for that reason, though I do not find the term very useful. (Augmented by what?) It turns out that the faces of the augmenting tetrahedron are coplanar with the adjacent sides of the octahedron. That's cool! But it is why this one gets the "N" designation (not strictly convex, unfairly denigrated as an interloper).

Number 4 is the pentagonal bipyramid and is not a face-joined union of any smaller deltahedra, unlike numbers 1,2,3,5. So it is a "prime" deltahedron in that sense.

Some photos of these deltahedra are at the links below, followed by some graphics and video.

Below are videos showing how four nets fold up to yield the five 7-vertex (10-faced) deltahedra — these are the only nets common to all five sets of nets of these deltahedra. (They are rendered in five rather random orientations, colored to suit a whim. The numbers below the images are just indices into my lists; please ignore.)

Common net 1 of 4 (click HERE for a version you can manipulate):

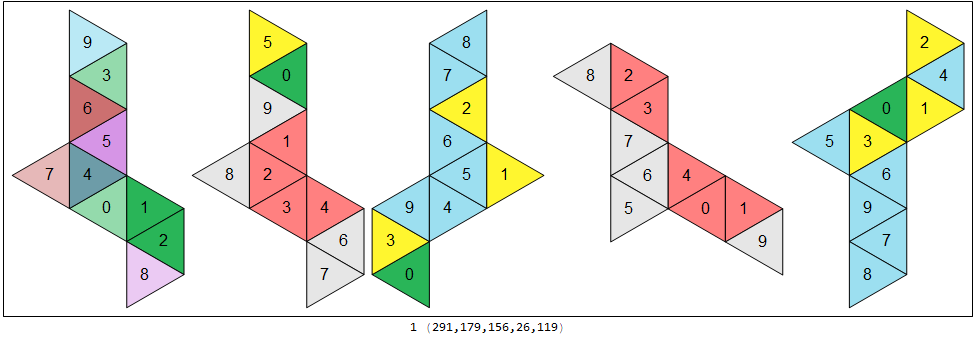
The net in action:

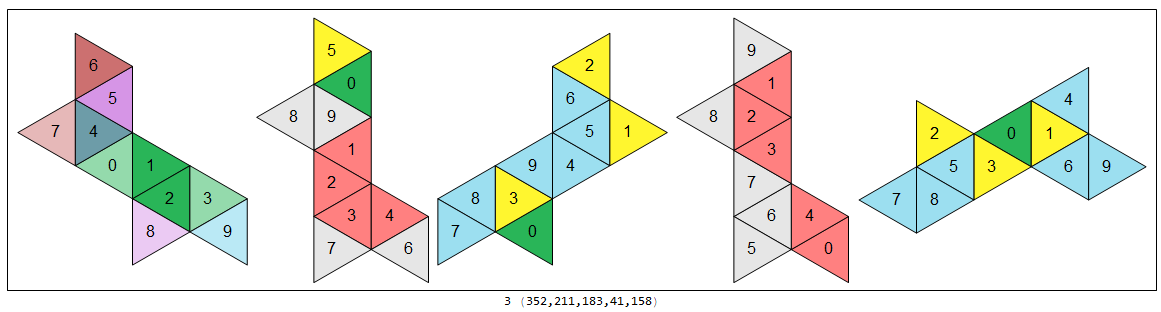
Common net 2 of 4:

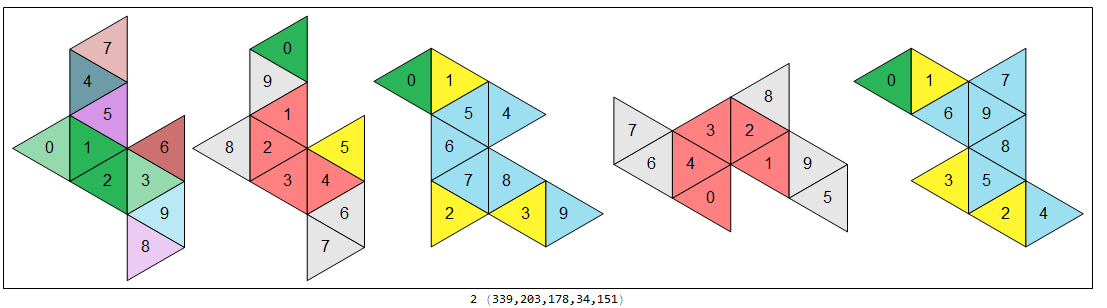
Common net 3 of 4:

Common net 4 of 4:

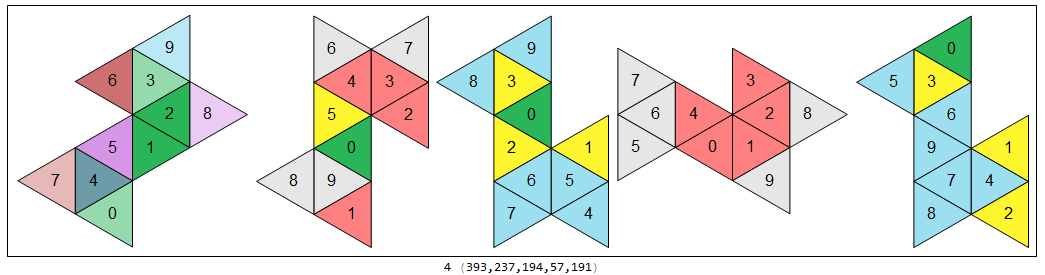
The four nets above, consisting as they do of 10 equilateral triangles apiece, are members of the family of 448 deciamonds. In particular, they are numbered 346, 337, 73, 316, respectively, on the website Polyomino, polyhex and polyiamond tiling of Joseph Myers. (The indices are buried in compressed postscript files.)

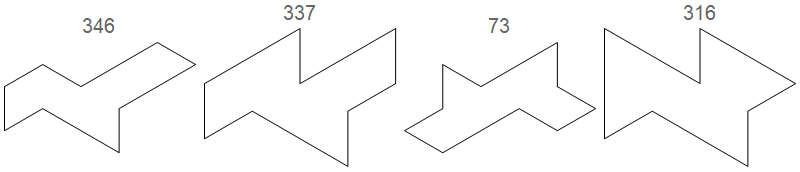
Each of the four nets above tiles the plane in at least one way. The fourth requires only translations. Here is one way to tile with the first; there is another (noticed by Yoshiaki Araki here) that does not require reflection.

I generated what I believe to be all the nets of the five 7-vertex deltahedra, the four above being special in that each of the four serves as a net of all five of our deltahedra. Each of the 448 deciamonds is represented at least once in the collection of nets! If I have crunched correctly, there are

452, 280, 203, 98, and 242

distinct nets for the respective five deltahedra above. Each net of a 7-vertex deltahedron corresponds to precisely one of 448 distinct deciamonds (or 10-iamonds), but not vice versa — notice that 448 is already less than the number (452) of alleged nets of 7V1, the first in the list of these five deltahedra. Altogether there are 624 distinct nets among the set of nets of the five. There are two reasons for this lack of one-to-one correspondence. One was mentioned above: Some of the nets fold into more than one deltahedron; the four nets shown above that can fold into each of the five deltahedra, for instance. The second reason is that there are many deciamonds that can fold into several distinct nets. Below is an example of that, in which deciamond #009 can be "cut" along different edges to fold into two different nets (and in this case, each of those nets fold into both 7V1 and 7V2).

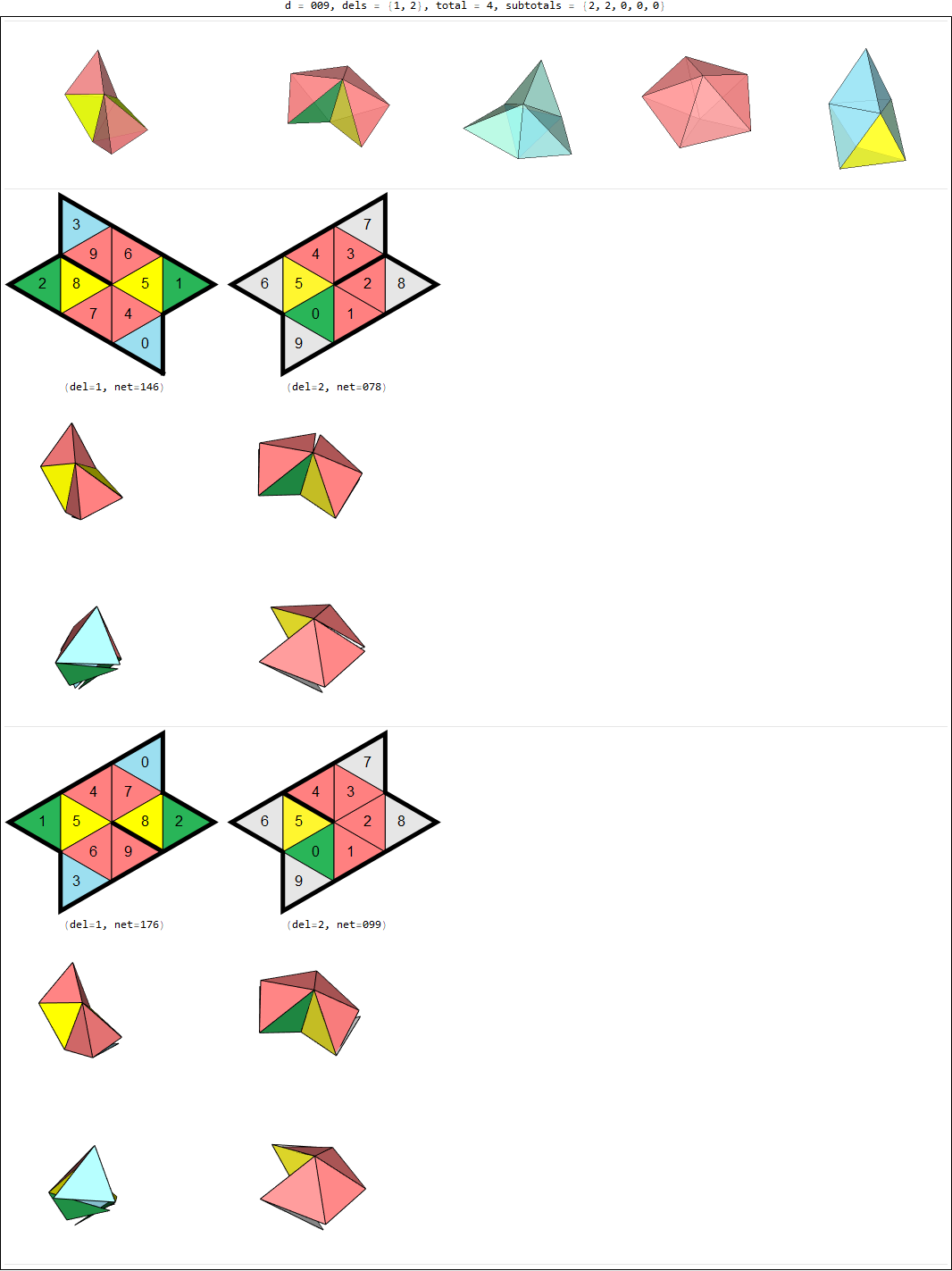
Here is a sort of "catalog" in a big, unwieldy PDF. An entry such as

d = 003, dels = {1, 2, 5}, total = 3, subtotals = {1, 1, 0, 0, 1}

indicates that deciamond number 003 (out of 448 in Joseph Myers' list) can serve as a net for deltahedras 1,2,5. That's followed by a list that just tells me which nets these are. An image like the one above is then at a link that incorporates the deciamond number:

cat1/commonNets-fiveDeltahedra-catalog1-003.png

If someone ever needs more decently presented info, I could try to do that. Meanwhile, do be amused and enlightened by Michael Stevens explaining the names and construction of the 8 official "strictly convex" deltahedra.

There are 16 distinct nets that fold into each of the three Tetraedervierlinge, the last one in the list being clearly pretty special. It is extremely special to me, but I'll save that story for later.

(*) An example of goofiness is attaching polyhedra along edges or points (as opposed to faces) to form new ones. For instance, attach two tetrahedra face to face to make a triangular bipyramid. Then attach a third tet along any edge of the bipyramid, but do not join faces. The result has 7 vertices and 10 faces. It is not rigid, since the 3rd tet can swivel about the connecting edge. And the figure has a disconnected interior (consisting of the disjoint interiors of the bipyramid and the 3rd tet). So let's reject such goofiness.

(**) If there are no holes, then Euler's formula V−E+F=2 holds, where V is the number of vertices (here V=7), E is the number of edges and F is the number of faces, which here are triangles. All faces being triangular, the number of edges is 3 per triangle, which would give us 3F edges. But the faces are are joined two per edge, so that would double-count the edges. The number of edges is therefore E=(3/2)F and we get 7−(3/2)F+F=2, which implies that F=10.

Euler's formula above, however, is for polyhedra of genus g=0, which is to say, polyhedra that are orientable (there is a consistent "outside" and "inside") and have no holes (like a doughnut). For orientable cases with g "holes" (or "handles"), Euler's formula is V−E+F=2−2g, where g>0. It is therefore algebraically possible for there to be more than 10 triangular faces. That is realizable for non-regular triangles. The genus 1 case is the Császár polyhedron, which has 14 triangular faces and 7 vertices. It was proved in 1959 that conjoining regular tetrahedra cannot be used to accomplish this, because regular tets cannot be strung together end-to-end to meet. (S. Świerczkowski (1959), On Chains of Regular Tetrahedra, Colloq. Math. vol. 7, pp. 9–10.) But eight octahedra can be chained together to give a torroidal deltahedron, as can a set of octahedra plus tetrahedra, which John H. Conway did to construct the toridal deltahedron of genus one with the smallest known set of triangular faces (36). Check it out here.

[TMKF] N. Tsuruta, J. Mitani, Y. Kanamori, Y. Fukui (2015), Random Realization of Polyhedral Graphs as Deltahedra, Journal for Geometry and Graphics, Volume 19 (2015), No. 2, 227–236.